Рядом Тейлора для функции f(x) называется степенной ряд вида:
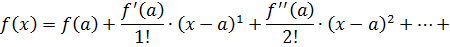
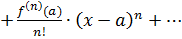 (27)
(27)
Если а=0, то получим частный случай ряда Тейлора:
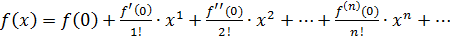 , (28)
, (28)
который называется рядом Маклорена.
Алгоритм нахождения области сходимости ряда.
1) Находим радиус сходимости по формуле (25)
2) Выписываем выражение, содержащее переменную х: 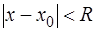 и решаем неравенство:
и решаем неравенство: 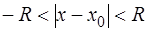 ;
; 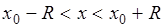 .
.
3) Подставляем левую часть неравенства в ряд вместо х, т.е. (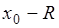 ) полученный ряд исследуем на сходимость.
) полученный ряд исследуем на сходимость.
4) Подставляем правую часть неравенства в ряд вместо х, т.е. (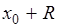 ) полученный ряд исследуем на сходимость.
) полученный ряд исследуем на сходимость.
5) Определим окончательные знаки на концах неравенства (26)
¾ если на границе ряд сходится, то знак не строгий 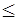 или
или 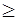 ;
;
¾ если на границе ряд расходится, то знак строгий < или >.
Рассмотрим типовые задания с подробными решениями и указаниями или методические рекомендации к выполнению задания.
Пример: Разложить в ряд Тейлора функцию: 1) 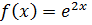 по степеням
по степеням 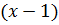 2)
2) 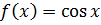 по степеням
по степеням 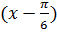
Решение: 1) Вычислим значения данной функции и её производных при 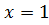 . Имеем:
. Имеем:
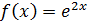 ,
, 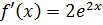 ,
, 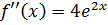 ,
, 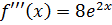 , …,
, …, 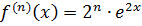
Получим: 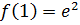 ,
, 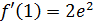 ,
, 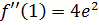 ,
, 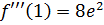 , …,
, …, 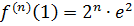 . Подставим эти значения в формулу ряда Тейлора:
. Подставим эти значения в формулу ряда Тейлора:
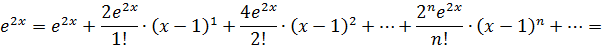
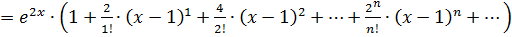 .
.
Промежуток сходимости ряда найдем: 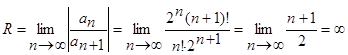
Следовательно, 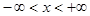
2) Вычислим значения данной функции и её производных при 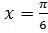 .
.
Имеем: 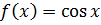 ,
, 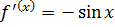 ,
, 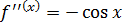 ,
, 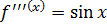 ,
, 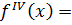
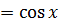
Получим: 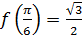 ,
, 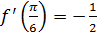 ,
, 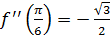 ,
, 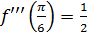 ,
, 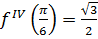 . Подставим эти значения в формулу ряда Тейлора:
. Подставим эти значения в формулу ряда Тейлора: 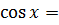
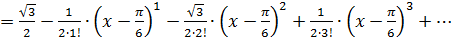 или
или
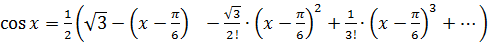 .
.
 2015-04-06
2015-04-06 1807
1807








