Хаотические колебания – это неупорядоченные движения, которые возникают в совершенно детерминированных нелинейных динамических системах различной природы и не связаны с действием на эти системы случайных внешних сил, в том числе и случайных шумов. Представляют собой новый класс движений, который связан часто с состоянием, получившим название странный аттрактор.
Аттрактор Лоренца – это трехмерная система нелинейных автономных дифференциальных уравнений первого порядка вида:
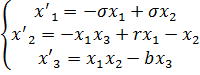 , (2.56)
, (2.56)
где 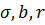 - параметры.
- параметры.
В результате численного интегрирования системы (2.56) Лоренц обнаружил, что при 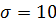 ,
, 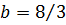 и
и  у этой динамической системы, с одной стороны, наблюдается хаотическое, нерегулярное поведение всех траекторий (рис. 2.8), а, с другой стороны, все траектории притягиваются к некоторому сложно устроенному множеству – аттрактору.
у этой динамической системы, с одной стороны, наблюдается хаотическое, нерегулярное поведение всех траекторий (рис. 2.8), а, с другой стороны, все траектории притягиваются к некоторому сложно устроенному множеству – аттрактору.
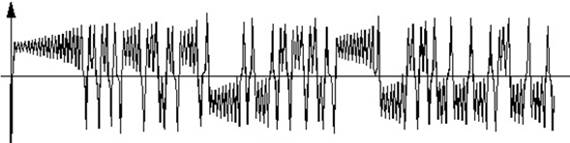
Рис. 2.8 – Зависимость координаты 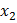 одной из траекторий от времени
одной из траекторий от времени
Зафиксируем в (2.56) 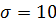 ,
, 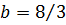 и будем увеличивать
и будем увеличивать 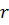 , начиная с нуля. При
, начиная с нуля. При 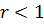 система Лоренца имеет асимптотически устойчивую в целом стационарную точку – начало координат. К ней притягиваются все траектории (рис. 2.9).
система Лоренца имеет асимптотически устойчивую в целом стационарную точку – начало координат. К ней притягиваются все траектории (рис. 2.9).
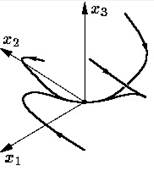
Рис. 2.9 – Траектории системы Лоренца
Когда 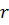 переваливает через единицу, происходит первая бифуркация. Начало координат теряет устойчивость и от него отделяются две новые устойчивые стационарные точки:
переваливает через единицу, происходит первая бифуркация. Начало координат теряет устойчивость и от него отделяются две новые устойчивые стационарные точки:
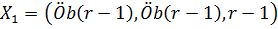 ,
,
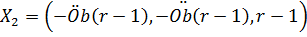 . (2.57)
. (2.57)
У линеаризованной в нулевой стационарной точке системы два отрицательных и одно положительное собственное значение. В соответствии с этим у нулевой стационарной точки есть двумерный входящий ус и одномерный выходящий (рис. 2.10).
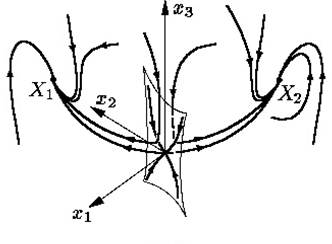
Рис. 2.10 – Траектории линеаризованной системы Лоренца
У линеаризованных в точках 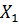 и
и 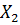 систем все собственные значения отрицательны. При возрастании параметра
систем все собственные значения отрицательны. При возрастании параметра 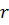 пара отрицательных собственных значений этих систем превращается в пару комплексно сопряженных собственных значений. Это, в частности, соответствует тому, что выходящие усы G1 и G2 нулевой стационарной точки начинают закручиваться как спирали около стационарных точек
пара отрицательных собственных значений этих систем превращается в пару комплексно сопряженных собственных значений. Это, в частности, соответствует тому, что выходящие усы G1 и G2 нулевой стационарной точки начинают закручиваться как спирали около стационарных точек 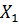 и
и 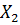 , соответственно (рис. 2.11).
, соответственно (рис. 2.11).
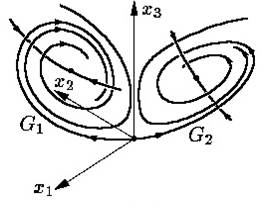
Рис. 2.11 – Траектории системы Лоренца при возрастании 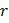
С дальнейшим ростом 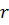 стационарные точки
стационарные точки 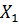 и
и 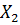 поднимаются выше (они лежат в плоскости
поднимаются выше (они лежат в плоскости 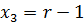 ), а спиралевидные траектории «разбухают». Это происходит до тех пор, пока при
), а спиралевидные траектории «разбухают». Это происходит до тех пор, пока при 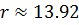 спирали, начинающиеся как выходящие усы нуля, попадают на его входящий ус, образуя две гомоклинические траектории Г1 и Г2 (рис. 2.12).
спирали, начинающиеся как выходящие усы нуля, попадают на его входящий ус, образуя две гомоклинические траектории Г1 и Г2 (рис. 2.12).
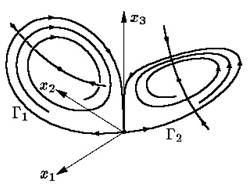
Рис. 2.12 – Гомоклинические траектории системы Лоренца
 2015-04-08
2015-04-08 2435
2435








