Спектрально-корреляционный анализ случайных сигналов. Теорема Винера-Хинчина

Сигнал - случайный физический процесс, отображающий передаваемую информацию.

Статистическая связь между двумя сечениями x(t) и x_t = x(t + t) случайного процесса характеризуется корреляционной функцией

B(t, t) = < (x - < x >) (x_t - < x_t >)> = < xx_t > - < x >< x_t >, (1)

где оператор статистического усреднения

¥

<... > = òò dx dx_t w(x, x_t; t, t + t), (2)

- ¥

и в нормированном виде (-1 £ R £ 1) - коэффициентом корреляции

R(t, t) = B(t, t) / (ss_t), (3)

где s² и s_t² - значения дисперсии (мощности флуктуаций) случайного процесса x в моменты времени t и t + t, соответственно, s² = B(t, 0) и s_t² = B(t + t, 0).

Для случайного стационарного процесса B(t, t) = B(t) и s = s_t = const. Характерный интервал времени, на котором происходит заметный спад (в несколько раз) функции корреляции, называется временемкорреляции t_к. Время корреляции можно оценить как

¥

t_к = 2 ò R²(t) dt. (4)

Если t > t_к, то корреляцией между выбранными сечениями случайного процесса можно пренебречь.

Корреляционную функцию стационарного процесса можно определить также, заменив статистическое усреднение временным. Вместо (1) получим

B(t) = lim (< x x_t >_T - < x >_T < x_t >_T). (5)

T® ¥

Представим флуктуационную компоненту: x(t) = x(t) - < x >, случайного процесса интегралом Фурье

¥

x(t) = ò x_w e^jwt dw, (6)

- ¥

где x_w случайная спектральная амплитуда.

Спектральная плотность мощности шума случайного процесса G(w) описывает распределение интегральной мощности (дисперсии s²) шума по спектру

¥

s² = B(0) = < x² > = ò G(w) dw. (7)

- ¥

Для случайных стационарных процессов справедлива теоремаВинера - Хинчина: Спектральная плотность G(w) процесса оказывается Фурье-транс-формантой корреляционной функции процесса

¥

G(w) = (2 p)^-1 ò B(t) e^-jwt dt, (8)

- ¥

- прямое преобразованиеВинера - Хинчина и

¥

B(t) = ò G(w) e^jwt dw, (9)

- ¥

- обратное преобразованиеВинера - Хинчина.

Спектральные амплитуды x_w и x_w’ случайного стационарного процесса d - коррелированны, так что

< x_w x_w’ > = G(w) d(w + w^’). (10)

Так как B(t) - четная функция: B(t) = B(-t), то, согласно (8) и (9), G(w) - также четная: G(w) = G(-w). Эффективнаяширинаспектрашума случайного процесса может быть оценена как

¥

Dw_ш = s⁴ / (4 ò G²(w) dw). (11)

С учетом (8) и (9) найдем связь между временем корреляции случайного процесса t_к из (1.16) и шириной спектра его флуктуаций Dw_ш из (11):

Dw_ш t_к = p. (12)

Из (11) следует, что чем больше эффективная ширина спектра шума случайного процесса, тем меньше время корреляции процесса.

Случайную реализацию х(t) можно разложить по детерминированным ортогональным функциям 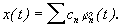Коэффициенты такого разложения с_n будут случайными величинами. Для гармонического разложения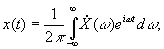 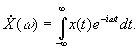Ввиду случайности спектральной плотности 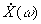и равенства нулю ее среднего значения при усреднении по всем реализациям при 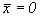(ввиду случайности и независимости фаз спектральных составляющих в различных реализациях) она не используется для характеристики случайного процесса. Поэтому для случайного процесса x(t) вводится понятие спектральной плотности мощности, связанной с автокорреляционной функцией преобразованием Фурье (соотношение Винера - Хинчина).

.

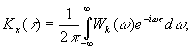
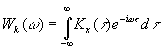Спектральная плотность мощности определяется из последнего соотношения по функции корреляции определяемой для эргодического процесса в пределах одной реализации:

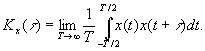
При нулевом среднем значении 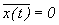имеем:

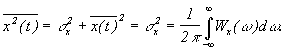
Чем шире энергетический спектр случайного процесса, тем быстрее меняется x(t) и меньше время корреляции, и наоборот.