Примеры решения задач. Пример 1. Дано очень тонкое кольцо, масса которого и радиус

Пример 1. Дано очень тонкое кольцо, масса которого 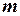и радиус 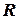. Найти моменты инерции относительно оси 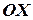, расположенной в плоскости кольца и проходящей через его центр.

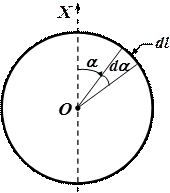Решение. Для вычисления момента инерции очень тонкого кольца воспользуемся соотношением (4.12а). Для этого кольцо разобьем на бесконечно малые части длиной 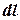и массой .

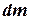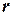
Введем линейную плотность кольца 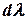. Выразим массу бесконечно малого участка через длину и его линейную плотность, получим следующее выражение:

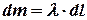. (1)

Длина участка 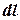является дугой окружности радиусом 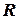, поэтому ее величина связана с бесконечно малым углом соотношением

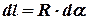. (2)

Из равенства (2) вместо 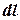подставим в равенство (1), получим выражение:

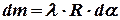. (4)

Обозначим расстояние от бесконечно малого участка до оси 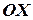через 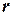, и и выразим его через радиус кольца

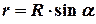. (5)

Запишем соотношение (4.12а) для момента инерции кольца относительно оси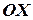

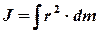. (6)

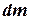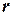Из равенств (4) и (5) вместо и подставим в равенство (6) получим

.

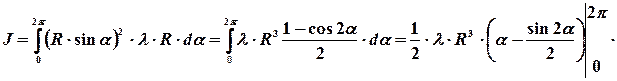Подставим пределы интегрирования, получим выражение для момента инерции кольца

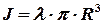. (7)

Выразим линейную плотность кольца 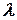через его массу 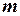и длину 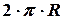, будем иметь выражение

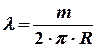. (8)

Из равенства (8) вместо линейной плотности 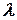подставим в равенство (7), получим окончательную формулу для момента инерции кольца относительно оси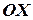

.

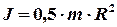[5] Пример 2. Радиус–вектор силы, выходящей из точки 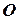, задан 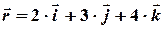, а вектор импульса 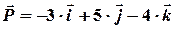. Найти: 1) вектор момента импульса; 2) величину момента импульса; 3) плечо вектора момента импульса относительно точки 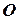3) проверить ортогональность (перпендикулярность) векторов 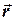, 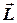и , .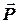

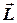Решение. Вектор момента импульса находим из соотношения (6.6.а)

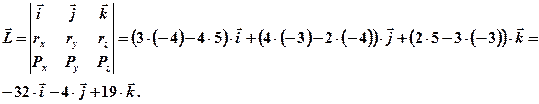
Величину момента импульса определяем через его проекции на оси координат по известной формуле

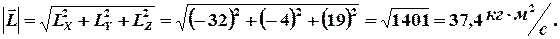
Зная, что величина момента импульса относительно точки равна произведению величины вектора импульса на его плечо относительно точки , находим плечо вектора момента импульса из равенства (4.7)

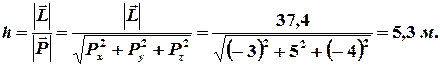
Известно, что скалярное произведение перпендикулярных векторов равно нулю. Используя этот факт, проверим ортогональность векторов 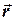, 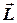и 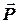, , 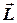для чего найдем их скалярные произведения

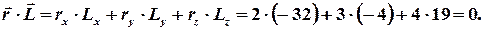
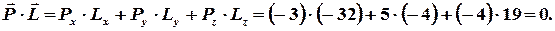
Таким образом скалярные произведения соответствующих пар векторов равны нулю, то 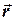, 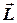и 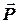, 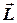являются ортогональными векторами.