Пример 11. Две гири массами 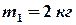 и
и 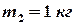 соединены нитью и перекинуты через блок массой
соединены нитью и перекинуты через блок массой 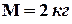 и радиусом
и радиусом 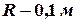 . Найти:1) угловое ускорение блока
. Найти:1) угловое ускорение блока 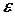 ; 2) ускорение
; 2) ускорение 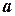 , с которым движутся гири; 3) силы натяжения
, с которым движутся гири; 3) силы натяжения 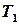 и
и 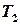 нитей, к которым подвешены гири; 4) силу реакции оси вращения
нитей, к которым подвешены гири; 4) силу реакции оси вращения 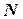 . Блок считать однородным диском. Массой, деформацией нитей и трением в блоке пренебречь.
. Блок считать однородным диском. Массой, деформацией нитей и трением в блоке пренебречь.
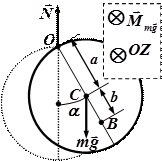
Решение. Изобразим силы, с которыми внешние тела действуют на блок. На блок действуют: Земля с силой тяжести 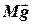 , ось вращения с силой реакции
, ось вращения с силой реакции 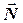 , нити с силами натяжения
, нити с силами натяжения 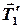 и
и 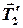 (см. рис.).
(см. рис.).
На гири действуют: Земля с силой тяжести 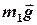 и
и 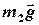 ; нити – с силами натяжения
; нити – с силами натяжения 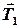 и
и 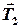 .
.
Выберем прямоугольную декартову систему координат так, как показано на рисунке. Используя правило «буравчика», определим и укажем направление векторов моментов сил натяжения нитей, действующих на блок; направление вектора его углового ускорения (см. вставку.–прямоугольник к рис). Моменты сил 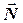 и
и 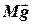 относительно оси вращения
относительно оси вращения  равны нулю, т.к. линии действия этих сил пересекают ось
равны нулю, т.к. линии действия этих сил пересекают ось  .
.
Запишем уравнения вращения тела вокруг закрепленной оси (4.34)
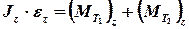 , (1).
, (1).
где 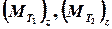 – моменты сил натяжения нити относительно оси вращения;
– моменты сил натяжения нити относительно оси вращения; 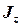 – момент инерции блока относительно оси вращения,
– момент инерции блока относительно оси вращения, 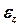 – проекция углового ускорения на ось
– проекция углового ускорения на ось  .
.
Учитывая, что момент инерции диска равен 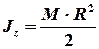 , и, кроме того,
, и, кроме того, 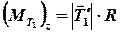 ,
, 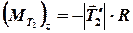 ,
, 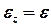 (см. вставку к рис.), получим следующее уравнение вращения блока вокруг оси
(см. вставку к рис.), получим следующее уравнение вращения блока вокруг оси  :
:
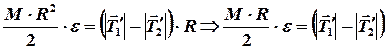 . (2)
. (2)
В данной задаче предполагается, что нить не скользит по блоку. Т.к нить не деформируется, то скорость и ускорение любой точки нити совпадают со скоростью и ускорением поступательного движения гирь, а также с тангенциальным ускорением блока,, т.е.
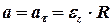 . (3)
. (3)
Из равенства (3) находим величину углового ускорения, и, подставим в равенство (2), получим следующее соотношение:
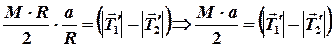 . (4)
. (4)
Запишем второй закон Ньютона для поступательного движения гирь с ускорением 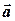 в проекции на ось
в проекции на ось 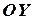
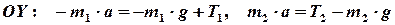 . (5)
. (5)
Для невесомых нитей векторы сил натяжения 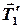 ,
, 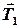 и
и 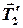 ,
, 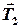 равны по величине, т.е.
равны по величине, т.е.
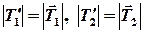 . (6)
. (6)
Выразим величины векторов сил 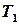 и
и 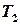 из уравнений (5), и подставим в равенство (4), получим соотношение, позволяющее найти ускорение движения гирь
из уравнений (5), и подставим в равенство (4), получим соотношение, позволяющее найти ускорение движения гирь
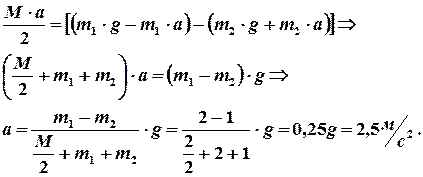
Величину углового ускорения найдем из формулы(3)
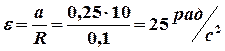 .
.
Силы натяжения нити определим из уравнений (5)
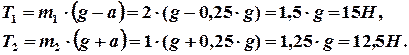
Силу реакции 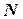 находим из условия равновесия оси вращения
находим из условия равновесия оси вращения 
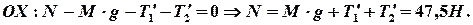
 Пример 12. Однородный диск радиусом
Пример 12. Однородный диск радиусом 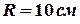 может свободно вращаться вокруг горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку
может свободно вращаться вокруг горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку 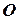 на нём. Диск отклонили на угол альфа и отпустили. Определить для начального момента времени величину вектора углового ускорения
на нём. Диск отклонили на угол альфа и отпустили. Определить для начального момента времени величину вектора углового ускорения 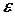 и тангенциального
и тангенциального 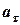 ускорения точки
ускорения точки 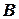 , находящейся на диске. Вычисления выполнить для следующего случая: 1)
, находящейся на диске. Вычисления выполнить для следующего случая: 1) 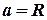 ,
, 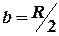 ,
, 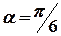 .
.
Решение. Изобразим все силы, с которыми внешние тела действует на диск, закрепленный в точке 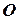 . На диск действует Земля с силой тяжести
. На диск действует Земля с силой тяжести 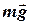 , точка приложения которой находится в центре масс, и, кроме того, на него действует ось с силой реакции, приложенной в точке
, точка приложения которой находится в центре масс, и, кроме того, на него действует ось с силой реакции, приложенной в точке 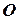 .
.
Для решения данной задачи используем уравнение вращения вокруг оси  (4.34).
(4.34).
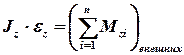 , (1)
, (1)
где 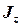 – момент инерции диска относительно закрепленной оси, проходящей через точку
– момент инерции диска относительно закрепленной оси, проходящей через точку 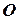 ;
; 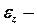 проекция углового ускорения диска на ось
проекция углового ускорения диска на ось  ;
; 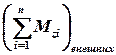 – сумма моментов внешних сил, действующих на диск.
– сумма моментов внешних сил, действующих на диск.
Момент инерции диска относительно оси  найдем по теореме Штейнера–Гюйгенса
найдем по теореме Штейнера–Гюйгенса
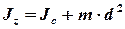 , (2)
, (2)
где 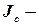 момент инерции диска относительно оси, проходящей через центр масс (точка
момент инерции диска относительно оси, проходящей через центр масс (точка 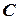 ),
), 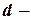 расстояние между осями. В данной задаче
расстояние между осями. В данной задаче 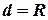 . С учетом этого находим момент инерции диска относительно оси
. С учетом этого находим момент инерции диска относительно оси 
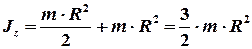 . (3)
. (3)
Момент силы реакции 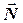 относительно оси
относительно оси  равен нулю, т.к. точка приложения этой силы лежит на оси вращения. Величина момента силы тяжести относительно оси вращения вычисляется по формуле
равен нулю, т.к. точка приложения этой силы лежит на оси вращения. Величина момента силы тяжести относительно оси вращения вычисляется по формуле
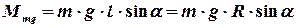 , (4)
, (4)
где 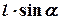 – плечо силы тяжести относительно оси вращения
– плечо силы тяжести относительно оси вращения  .
.
С учетом равенств (3) и (4) уравнение движения тела примет вид
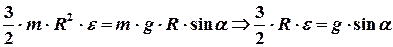 .
.
Из последнего соотношения находим величину вектора углового ускорения
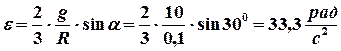 .
.
Величину тангенциального ускорения точки 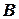 находим из следующего кинематического соотношения:
находим из следующего кинематического соотношения:
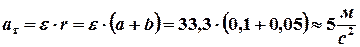 .
.
 Пример 13. Однородный диск радиусом
Пример 13. Однородный диск радиусом 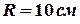 и массой
и массой 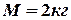 может свободно вращаться вокруг горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку
может свободно вращаться вокруг горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку 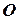 на нём. В диск попадает горизонтально летящая пуля массой
на нём. В диск попадает горизонтально летящая пуля массой 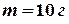 , вектор скорости которой направлен в точку
, вектор скорости которой направлен в точку 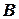 . Диск вместе с пулей отклоняются на угол
. Диск вместе с пулей отклоняются на угол 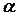 . Определить величину начальной скорости пули. Пулю считать материальной точкой. Вычисления выполнить для следующего случая: 1)
. Определить величину начальной скорости пули. Пулю считать материальной точкой. Вычисления выполнить для следующего случая: 1) 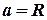 ,
, 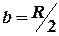 ,
, 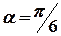 .
.
Решение. Изобразим все силы, с которыми внешние тела действует на диск, закрепленный в точке 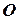 . На диск действует Земля с силой тяжести
. На диск действует Земля с силой тяжести 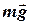 , точка приложения которой находится в центре масс, и, кроме того, на него действует ось с силой реакции, приложенной в точке
, точка приложения которой находится в центре масс, и, кроме того, на него действует ось с силой реакции, приложенной в точке 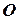 .
.
Для решения данной задачи используем уравнение моментов для системы «пуля–диск» в проекции на ось  . Учтем, что ось
. Учтем, что ось  проходит через точку
проходит через точку 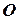 , и направлена перпендикулярно плоскости рисунка к нам. Запишем уравнение моментов для системы «пуля–диск» в проекции на ось
, и направлена перпендикулярно плоскости рисунка к нам. Запишем уравнение моментов для системы «пуля–диск» в проекции на ось 
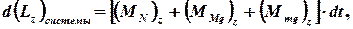 (1)
(1)
где 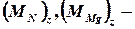 моменты силы реакции и силы тяжести диска относительно оси
моменты силы реакции и силы тяжести диска относительно оси  ;
; 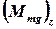 – момент силы тяжести пули относительно той же оси. Линии действия сил реакции
– момент силы тяжести пули относительно той же оси. Линии действия сил реакции 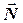 и силы тяжести диска
и силы тяжести диска 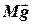 пересекают ось
пересекают ось  , поэтому моменты этих сил относительно этой оси равны нулю. С учетом этого равенство (1) упростится и примет вид
, поэтому моменты этих сил относительно этой оси равны нулю. С учетом этого равенство (1) упростится и примет вид
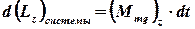 . (2)
. (2)
В данной задаче время взаимодействия пули с диском является бесконечно малой величиной, т.е. 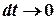 , отсюда вытекает, что произведение момента силы тяжести пули относительно оси вращения на время взаимодействия также является бесконечно малой величиной (
, отсюда вытекает, что произведение момента силы тяжести пули относительно оси вращения на время взаимодействия также является бесконечно малой величиной ( 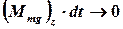 ). Следовательно, бесконечно малое изменение момента системы«пуля–диск» относительно оси вращения равно нулю, т.е.
). Следовательно, бесконечно малое изменение момента системы«пуля–диск» относительно оси вращения равно нулю, т.е. 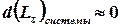 . С учетом этого запишем закон сохранения проекции момента импульса системы в проекции на ось вращения
. С учетом этого запишем закон сохранения проекции момента импульса системы в проекции на ось вращения
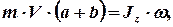 (3)
(3)
где 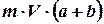 – момент импульса пули относительно оси
– момент импульса пули относительно оси  до взаимодействия с диском;
до взаимодействия с диском; 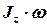 – момент импульса системы «пуля–диск» после взаимодействия;
– момент импульса системы «пуля–диск» после взаимодействия; 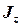 – момент инерции системы «пуля–диск» относительно оси вращения. При вычислении момента инерции системы «пуля–диск» для диска применим теорему Штейнера–Гюйгенса, а момент инерции пули рассчитаем по формуле момента инерции для материальной точки, т.е.
– момент инерции системы «пуля–диск» относительно оси вращения. При вычислении момента инерции системы «пуля–диск» для диска применим теорему Штейнера–Гюйгенса, а момент инерции пули рассчитаем по формуле момента инерции для материальной точки, т.е.
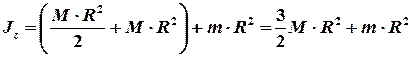 . (4)
. (4)
С учетом равенства (4) соотношение (3) примет вид
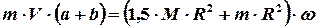 (5)
(5)
На систему «пуля–диск» действуют внешние сил: 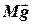 – сила тяжести диска;
– сила тяжести диска; 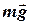 – сила тяжести пули. Эти силы являются консервативными. И, кроме того, действует сила реакции
– сила тяжести пули. Эти силы являются консервативными. И, кроме того, действует сила реакции 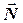 , точка приложения которой неподвижна, и, следовательно, работа этой силы равна нулю. Отсюда вытекает то, что механическая энергия системы «пуля–диск» после взаимодействия не зависит от времени. Запишем закон сохранения механической энергии системы после попадания пули в диск
, точка приложения которой неподвижна, и, следовательно, работа этой силы равна нулю. Отсюда вытекает то, что механическая энергия системы «пуля–диск» после взаимодействия не зависит от времени. Запишем закон сохранения механической энергии системы после попадания пули в диск
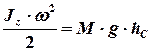 , (6)
, (6)
где 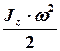 – начальная кинетическая энергия системы;
– начальная кинетическая энергия системы; 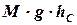 – потенциальная энергия системы «пуля–диск» в момент максимального отклонения от положения равновесия;
– потенциальная энергия системы «пуля–диск» в момент максимального отклонения от положения равновесия; 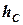 – высота центра масс диска в этот момент. Т.к. масса пули является бесконечно малой величиной по сравнению с массой диска, то ее потенциальной энергией мы пренебрегаем.
– высота центра масс диска в этот момент. Т.к. масса пули является бесконечно малой величиной по сравнению с массой диска, то ее потенциальной энергией мы пренебрегаем.
Высота центра масс диска связана с его радиусом соотношением
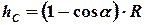 . (7)
. (7)
Из соотношений (4) и (7) вместо 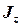 и
и 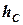 подставим в равенство (6), получим следующее уравнение:
подставим в равенство (6), получим следующее уравнение:
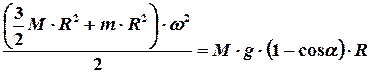 . (8)
. (8)
Уравнение (8) позволяет найти величину угловой скорости системы «пуля–диск»
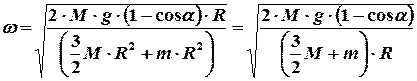 . (9)
. (9)
Подставим в уравнение (5) выражение для угловой скорости, получим следующее выражение:
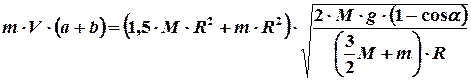 . (10)
. (10)
Полученное равенство позволяет нам определить искомую величину, а именно, скорость пули до столкновения с диском
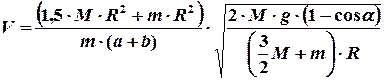 .
.
Вычислим величину вектора скорости, для чего подставим в последнее равенство численные значения входящих в него величин
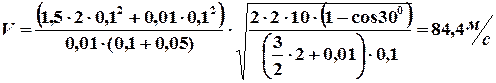 .
.
Пример 14. Человек массой 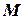 стоит на расстоянии
стоит на расстоянии 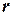 от оси горизонтального однородного диска массой
от оси горизонтального однородного диска массой 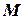 и радиусом
и радиусом 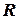 , который может свободно вращаться вокруг неподвижной вертикальной оси, проходящей через его центр. В некоторый момент времени человек начал двигаться по краю диска, совершил перемещение на угол
, который может свободно вращаться вокруг неподвижной вертикальной оси, проходящей через его центр. В некоторый момент времени человек начал двигаться по краю диска, совершил перемещение на угол 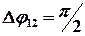 относительно диска и остановился. Пренебрегая размерами человека, найти угол, на который повернулся диск к моменту остановки человека.
относительно диска и остановился. Пренебрегая размерами человека, найти угол, на который повернулся диск к моменту остановки человека.
Решение. Для решения данной задачи выберем ось  и совместим ее с осью вращения системы «человек–диск» (см. рис.). Изобразим силы, с которыми внешние тела действуют на данную систему. На человека действует сила тяжести
и совместим ее с осью вращения системы «человек–диск» (см. рис.). Изобразим силы, с которыми внешние тела действуют на данную систему. На человека действует сила тяжести 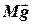 со стороны Земли. На диск действует сила тяжести
со стороны Земли. На диск действует сила тяжести 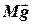 со стороны Земли, сила реакции
со стороны Земли, сила реакции 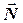 со стороны подставки, и, кроме того, в подшипниках данной системы возникает пара сил, создающая момент сил
со стороны подставки, и, кроме того, в подшипниках данной системы возникает пара сил, создающая момент сил 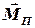 , противодействующий моменту силы тяжести человека (как в балке с жесткой заделкой в стенку) (см. вставку к рисунку). Относительно оси
, противодействующий моменту силы тяжести человека (как в балке с жесткой заделкой в стенку) (см. вставку к рисунку). Относительно оси  моменты силы тяжести платформы и силы реакции равны нулю, т.к. их линии действия лежат на оси вращения. Момент силы тяжести человека относительно оси
моменты силы тяжести платформы и силы реакции равны нулю, т.к. их линии действия лежат на оси вращения. Момент силы тяжести человека относительно оси  и момент пары сил в подшипниках перпендикулярны этой оси (см. вставку), следовательно, проекции векторов
и момент пары сил в подшипниках перпендикулярны этой оси (см. вставку), следовательно, проекции векторов 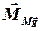 и
и 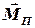 на эту ось будут равны нулю. Отсюда вытекает то, что проекция момента импульса системы «человек–диск» на ось
на эту ось будут равны нулю. Отсюда вытекает то, что проекция момента импульса системы «человек–диск» на ось  будет оставаться постоянной. Учтем, что начальный момент импульса рассматриваемой системы равен нулю, запишем закон сохранения момента импульса на ось
будет оставаться постоянной. Учтем, что начальный момент импульса рассматриваемой системы равен нулю, запишем закон сохранения момента импульса на ось 
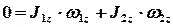 , (1)
, (1)
где 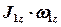 – проекция момента импульса человека на ось;
– проекция момента импульса человека на ось; 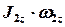 – проекция момента импульса диска на ось
– проекция момента импульса диска на ось  ;
; 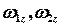 – проекции угловой скорости вращения человека и диска соответственно относительно Земли.
– проекции угловой скорости вращения человека и диска соответственно относительно Земли.
С учетом выбранного направления оси  получим следующее выражения:
получим следующее выражения:
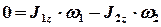 . (2)
. (2)
Угловые скорости человека и диска относительно Земли связаны соотношением
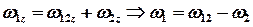 , (3)
, (3)
где 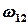 – величина вектора угловой скорости человека относительно диска.
– величина вектора угловой скорости человека относительно диска.
Из равенства (3) вместо величины вектора угловой скорости человека относительно Земли 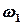 подставим в равенство (2) его выражение, получим следующее уравнение:
подставим в равенство (2) его выражение, получим следующее уравнение:
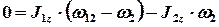 . (4)
. (4)
Учитывая, что 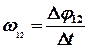 ,
, 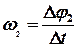 , и
, и 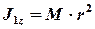 ,
, 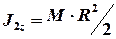 , перепишем равенство (4) в следующем виде:
, перепишем равенство (4) в следующем виде:
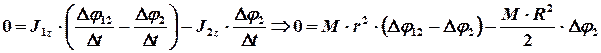 .
.
Из последнего уравнения находим угол поворота диска относительно Земли
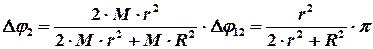 .
.
 2015-04-30
2015-04-30 2497
2497
