Если дифференциальная функция (плотность) распределения вероятностей случайной величины 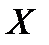 выражается функцией
выражается функцией
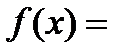
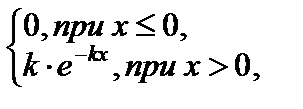 (4.1)
(4.1)
где k > 0 – параметр, то говорят, что случайная величина X имеет показательное распределение.
Функция распределения такой случайной величины имеет вид
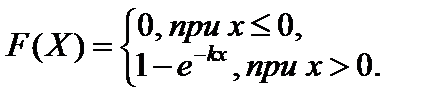 (4.2)
(4.2)
Теорема. Числовые характеристики случайной величины, распределенной по показательному закону, определяются по формулам:
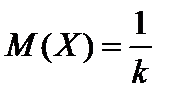 ;
; 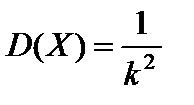 ;
; 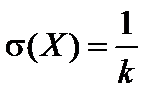 .
.
Пример 4.2. Написать дифференциальную и интегральную функции показательно распределенной случайной величины X, если параметр k = 6.
Решение
Подставив k в соотношения (4.1) и (4.2), получим
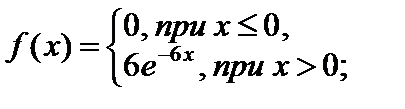
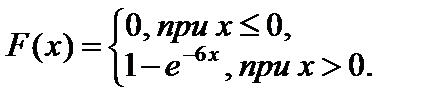
Пример 4.3. Непрерывная случайная величина X распределена по показательному закону, заданному интегральной функцией
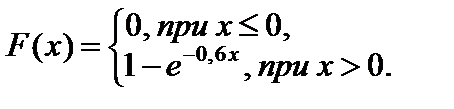
Найти вероятность того, что в результате испытания случайная величина попадет в интервал (2; 5).
Решение
Воспользуемся формулами вероятности попадания в интервал (a; b) случайной величины X:
1. через F(x):
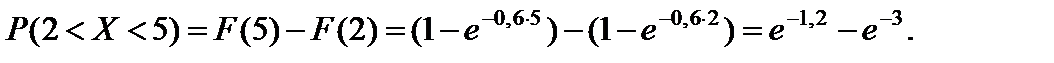
2. через f(x)
Найдем f(x):
f(x) = F'(x) = 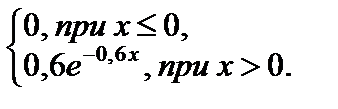
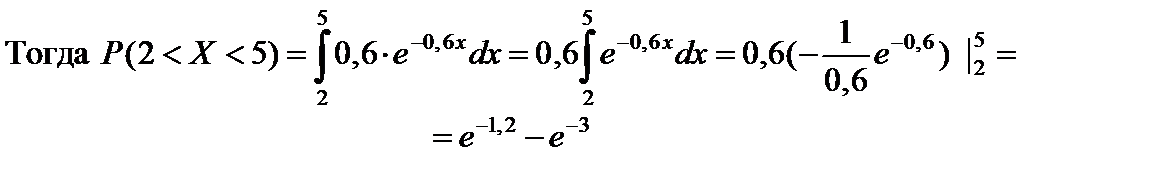
Ответ: e – 1,2 – e – 3.
Пример 4.4. Найти математическое ожидание, дисперсию и сред-нее квадратическое отклонение показательного распределения, заданного дифференциальной функцией
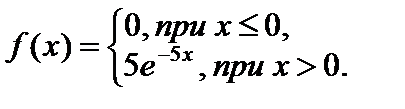
Решение
Подставив k = 5 в формулы для вычисления математического ожидания, дисперсии и среднего квадратического отклонения, получим:
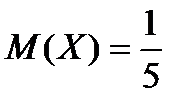 ,
, 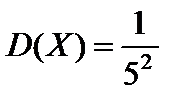 ,
, 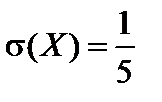 .
.
Тест 4.15. Параметр k показательного распределения, заданного дифференциальной функцией:
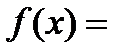
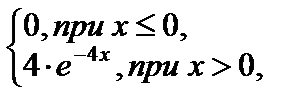
равен:
1) 2;
2) 0;
3) 1;
4) 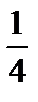 ;
;
5) 4.
Тест 4.16. Дисперсия показательного распределения, заданного дифференциальной функцией:
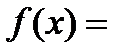
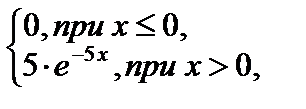
равна:
1) 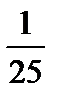 ;
;
2) 5;
3) 1;
4) 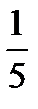 ;
;
5) –5.
Тест 4.17. Математическое ожидание, дисперсия непрерывной случайной величины Х, распределенной по показательному закону
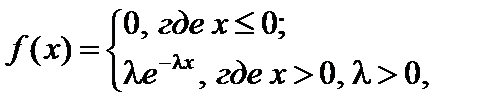
равны:
1) l, l;
2) 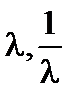 ;
;
3) 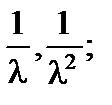
4) 1,0;
5) 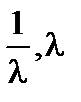 .
.
Тест 4.18. Случайная величина X имеет показательное распределение, если ее дифференциальная функция (плотность) распределения равна:
1) 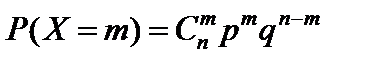 ;
;
2) 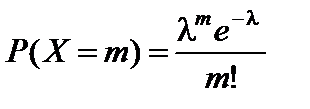 ;
;
3) 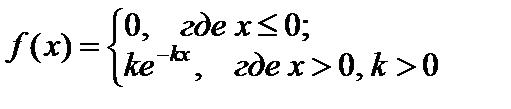 ;
;
4) 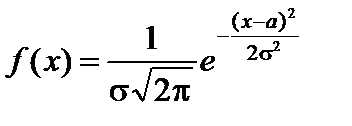 ;
;
5) 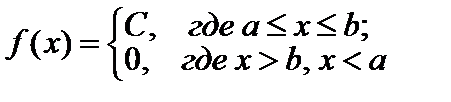 .
.
 2015-04-20
2015-04-20 2695
2695
