2015-04-20
1831
Двумерной случайной величиной называется случайная величина (X; Y), задаваемая рядом распределения с двумя входами
| y x | y 1 | … | ym |
| x 1 | p 11 | … | p 1 m |
| … | … | … | … |
| xn | pn 1 | … | pnm |
Так как события { x = xi; y = yj } образуют полную группу, то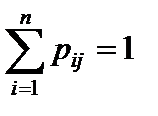 
.
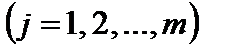Пример 5.1. Двумерная случайная величина задана рядом распределения.
| y x | y 1 = 1 | y 2 = 2 |
| x 1 = 0 | 0,1 | 0,4 |
| x 2 = 3 | 0,2 | p (x 2; y 2) |
Какова вероятность p (x 2; y 2)?
Решение
p (x 2; y 2) = 1 – (0,1 + 0,4 + 0,2) = 0,3.
Ответ: 0,3.
Тест 5.1. Двумерная случайная величина задана рядом распределения
 x
| y 1 = 1 | y 2 = 2 |
| x 1 = 0 | 0,1 | 0,4 |
| x 2 = 3 | 0,2 | p (x 2; y 2) |
Вероятность p (x 2; y 2) равна:
1) 0;
2) 0,3;
3) 0,2;
4) 0,1;
5) 0,4.
Пример 5.2. Двумерная случайная величина задана рядом распределения
| x y | y 1 = 1 | y 2 = 2 |
| x 1 = 0 | 0,1 | 0,4 |
| x 2 = 3 | 0,2 | 0,3 |
Записать ряд распределения случайной величины X.
Решение
| X | ||
| pi | 0,1 + 0,4 | 0,2 + 0,3 |
Тест 5.2. Двумерная дискретная величина (X, Y) задана законом распределения
| ||
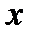| 0,1 | 0,3 | |
| 0,4 | p (x 2; y 2) |
Вероятность p (x 2; y 2) равна:
1) 1;
2) 0,7;
3) 0,6;
4) 0,2;
5) 0.
Тест 5.3. Двумерная случайная величина задана рядом распределения
|
|
|
|
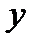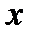| y 1 = 1 | y 2 = 2 |
| x 1 = 0 | 0,1 | 0,4 |
| x 2 = 3 | 0,2 | 0,3 |
Вероятность появления x 2 = 3 равна:
1) 0;
2) 0,1;
3) 0,2;
4) 0,3;
5) 0,5.
Тест 5.4. Двумерная случайная величина задана рядом распределения
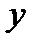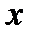| y 1= 1 | y 2= 2 |
| x 1= 0 | 0,1 | 0,4 |
| x 2= 3 | 0,2 | 0,3 |
Вероятность появления у 1 = 1 равна:
1) 0;
2) 0,1;
3) 0,2;
4) 0,3;
5) 0,5.
Зависимость между случайными величинами x и y описывает корреляционный момент:
.
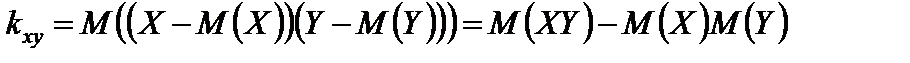Коэффициентом корреляции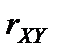 
случайных величин X и Y, между которыми предполагается линейная корреляционная связь, называется величина, определяемая по формуле
.
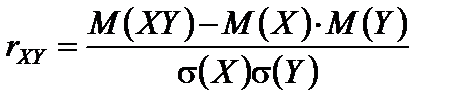Корреляционной матрицей называется матрица вида
.
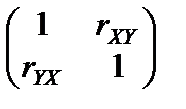Корреляционная матрица также устанавливает взаимосвязь наборов выборочных данных по величине:
· при 0 < rXY < 1 большим значениям случайной величины X соответствуют большие значения случайной величины Y;
· при –1 < rXY < 0 большим значениям случайной величины X соответствуют меньшие значения случайной величины Y (или наоборот);
· при rX = 0данные двух случайных величин некоррелированы;
· при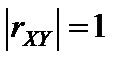 
существует линейная функциональная зависимость между случайными величинами X и Y.
Пример 5.3. Корреляционный момент kxy = 270. Какова зависимость между X и Y?
Решение
Так как kxy имеет размерность, то можно говорить лишь о прямой зависимости между Х и Y.
Пример 5.4. Коэффициент корреляции rXY = – 0,375. Какова зависимость между Х и Y?
Решение
По коэффициенту можно судить о виде зависимости и ее силе. Так как rXY = – 0,375 < 0, то зависимость обратная, так как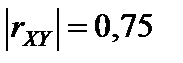 
, то связь между Х и Y высокая.
Тест 5.5. Известно, что kxy = 2,75, s Х = 3,1, s Y = 2,5. Коэффициент корреляции равен:
|
|
|
1) 
;
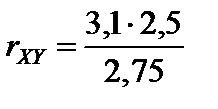2) 
;
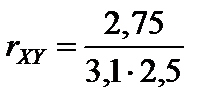3) 
.
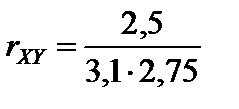Тест 5.6. Коэффициент корреляции rXY = 0. Тогда зависимость между X и Y:
1) прямая линейная;
2) обратная линейная;
3) данные двух случайных величин некоррелированы.
Тест 5.7. Коэффициент корреляции rXY = 1. Тогда зависимость между X и Y:
1) прямая линейная;
2) обратная линейная;
3) данные двух случайных величин некоррелированы;
4) функциональная прямая линейная.
Тест 5.8. Коэффициент корреляции rXY = –1. Тогда зависимость между X и Y:
1) прямая линейная;
2) обратная линейная;
3) данные двух случайных величин некоррелированы;
4) функциональная обратная линейная.
Вопросы для самоконтроля
1. Двумерные случайные величины.
2. Корреляционный момент.
3. Коэффициент корреляции.
