Теорема. Каково бы ни было 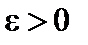 для любой случайной величины Х, дисперсия которой конечна, имеет место неравенство Чебышева
для любой случайной величины Х, дисперсия которой конечна, имеет место неравенство Чебышева
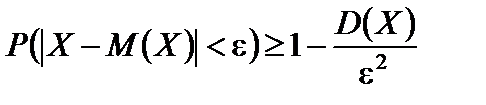 . (6.3)
. (6.3)
Известно, что сумма вероятностей двух противоположных событий равна единице, следовательно,
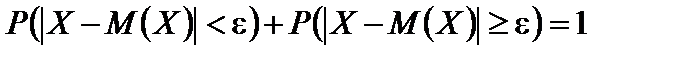
или
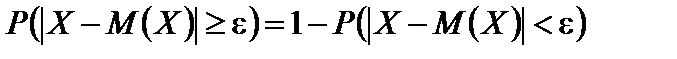 .
.
Отсюда и из неравенства (6.3) следует, что
 . (6.4)
. (6.4)
Неравенство (6.4) называют второй формой неравенства Чебышева.
Тест 6.5. чтобы для случайной величины Х имело место неравенство Чебышева, она должна обладать свойством:
1) математическое ожидание M (X) конечно;
2) дисперсия D (X) конечна;
3) M (X) не существует;
4) D (X) = ¥;
5) M (X) = ¥.
Пример 6.3. Случайная величина X имеет дисперсию D (X) = 1,66. Используя неравенство Чебышева, оценить вероятность того, что случайная величина X отличается от своего математического ожидания по абсолютной величине менее чем на 2.
Решение
По условию D (X) = 1,66, e = 2. Применяя неравенство (6.3), находим 
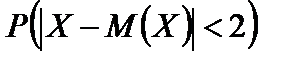
 .
.
Ответ: 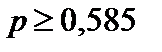 .
.
Пример 6.4. Случайная величина X имеет дисперсию D (X) = 0,001.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина X отличается от своего математического ожидания по абсолютной величине не менее чем на 0,1.
Решение
По условию D (X) = 0,001, e = 0,1.
Применяя неравенство (6.4), находим
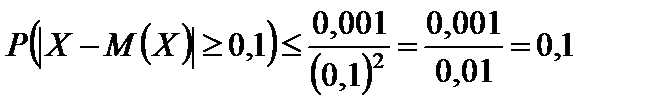 .
.
Ответ: 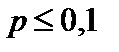 .
.
Тест 6.6. Случайная величина X имеет дисперсию D (X) = 1620. Оценкой вероятности того, что случайная величина X отличается от своего математического ожидания по абсолютной величине менее чем на 200, по неравенству Чебышева является выражение:
1) 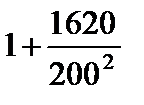 ;
;
2) 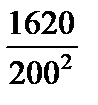 ;
;
3) 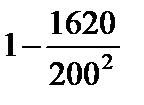 ;
;
4) 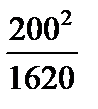 ;
;
5) 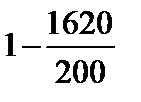 .
.
Тест 6.7. Случайная величина X имеет дисперсию D (X) = 0,004. Оценкой вероятности того, что случайная величина X отличается от своего математического ожидания по абсолютной величине не менее чем на 0,2, по неравенству Чебышева является выражение:
1) 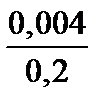 ;
;
2) 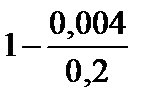 ;
;
3) 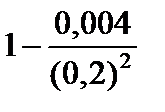 ;
;
4) 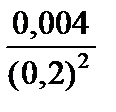 ;
;
5) 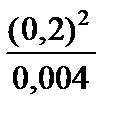 .
.
 2015-04-20
2015-04-20 4258
4258
