В задачах 1–20 даны координаты вершин треугольника ABC. Сделать чертёж и найти: 1) длины и уравнения сторон треугольника; 2) уравнение высоты AD; 3) уравнение медианы СМ; 4) уравнение вписанной окружности.
| 1. A (8; –1); B (–8; 11); С (–1; –13) | 2. A (–10; 5); B (6; –7); С (–1; 17) |
| 3. А (10; –4); B (–6; 8); С (1; –16) | 4. A (3; 2); B (–13; –10); C (–6; 14) |
| 5. A (7; 4); B (–9; –8); С (–2; 16) | 6. A (7; 3); B (–9; –9); С (–2; 15) |
| 7. A (–13; 3); B (3; –9); C (–4; 15) | 8. A (12; –2); B (–4; –14); С (3; 10) |
| 9. A (7; 5); B (–9; –7); С (–2; 17) | 10. A (13; 7); B (–3; –5); C (4; 19) |
| 11. A (10; 4); B (–6; –8); С (1; 16) | 12. A (3; 1); B (–13; –11); C (–6; 13) |
| 13. A (3; 4); B (–13; –8); C (–6; 16) | 14. A (5; 7); B (–11; –5); C (–4; 19) |
| 15. A (–2; 3); B (–18; –9); C (–11; 15) | 16. A (10; 7); B (–6; –5); C (1; 19) |
| 17. A (11,0); В (–5; –12); C (2; 12) | 18. A (9; –3); B (–7; –15); C (0; 9) |
| 19. A (10; 7); B (–6; –5); C (1; 19) | 20. A (10; 3); B (–6; 15); C (1; –9) |
В задачах 21–40 даны координаты вершин пирамиды А 1 А 2 А 3 А 4. Найти: 1) длину ребра А 1 А 2; 2) угол между рёбрами А 1 А 2и А 1 А 4; 3) угол между ребром А1А4 и гранью A 1 A 2 A 3; 4) площадь грани А 1 А 2 А 3; 5) объём пирамиды; 6) уравнения прямой А 1 А 2; 7)уравнение плоскости A 1 A 2 A 3; 8) уравнения высоты, опущенной из вершины А 4на грань А 1 А 2 А 3.Сделать чертёж.
21. A 1(4; 2; 5), A 2(0; 7; 2), А 3(0; 2; 7), А 4(1; 5; 0).
22. A 1(4; 4; 10), A2 (4; 10; 2), A 3(2; 8; 4), A 4(9; 6; 4).
23. A 1(4; 6; 5), A 2(6; 9; 4), A 3(2; 10; 10), A 4(7; 5; 9).
24. A 1(3; 5; 4), A 2(8; 7; 4), A 3(5; 10; 4), A 4(4; 7; 8).
25. A 1(10; 6; 6), A 2(–2; 8; 2), A 3(6; 8; 9), A 4(7; 10; 3).
26. A 1(1; 8; 2), A 2(5; 2; 6), A 3(5; 7; 4), A 4(4; l0; 9).
27. A 1(6; 6; 5), A 2(4; 9; 5), A 3(4; 6; 11), A 4(6; 9; 3).
28. A 1(7; 2; 2), A 2(5; 7; 7), A 3(5; 3; 1), A 4(2; 3; 7).
29. A 1(8; 6; 4), A 2(10; 5; 5), A 3(5; 6; 8), A 4(8; 10; 7).
30. A 1(7; 7; 3), A 2(6; 5; 8), A 3(3; 5; 8), A 4(8; 4; 1).
31. A 1(5; –2; 6), A 2(1; –7; 3), A 3(1; –2; 8), A 4(2; –5; 1).
32. A 1(–4; 2; 8), A 2(–4; 8; 0), A 3(–2; 6; 2), A 4(–9; 4; 2).
33. A 1(2; 4; –5), A 2(4; 7; –4), A 3(0; 8; –10), A 4(5; 3; –9).
34. A 1(0; 2; –4), A 2(5; 4; –4), A 3(2; 7; –4), A 4(1; 4; –8).
35. A 1(9; 5; –6), A 2(–3; 7; –2), A 3(5; 7; –9), A 4(6; 9; –3).
36. A 1(–1; 5; –1), A 2(–5; –1; 3), A 3(–5; 4; 1), A 4(–4; 7; 6).
37. A 1(4; 4; 3), A 2(2; 7; 3), A 3(2; 4; 9), A 4(4; 7; 1).
38. A 1(5; 0; –2), A 2(3; 5; –7), A 3(3; 1; –1), A 4(0; 1; –7).
39. A 1(5; 3; 1), A 2(7; 2; 2), A 3(2; 3; 5), A 4(5; 7; 4).
40. A 1(6; –7; 2), A 2(5; –5; 7), A 3(2; –5; 7), A 4(7; –4; 0).
В задачах 41–49 составить уравнение геометрического места точек, равноудалённых от точки А (х 1, у 1)и прямой у = b. Полученное уравнение привести к простейшему виду. Сделать чертеж.
| 41. A (2, 6), у = 2. | 42. A (–1, –4), у = –2. | 43. А (2,–3), у = 1. |
| 44. А (3, –5), у = –1 | 45. А (3, 5), у = 1. | 46. A (–4, 2), у = –2. |
| 47. A (–2, 5), у = 1. | 48. А (–2, 3), y =–1 | 49. А (2, –1), у = 3. |
В задачах 50–60 составить уравнение геометрического места точек, отношение расстояний которых до точки А (х, у)и прямой х = а равно числу b. Сделать чертеж.
| 50. A (12, 0), х = 3, b = 2. | 51. A (–2, 0), x = –4,5, 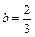 . .
|
52. A (8, 0), х = 4, 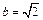
| 53. A (–9, 0), x = –4, 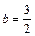 . .
|
54. A(3, 0), х = 12, 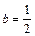 . .
| 55. A (10, 0), x = 2, 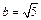 . .
|
56. A (–12, 0), 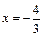 , b = 3. , b = 3.
| 57. A (–1, 0), x = –4, 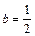 . .
|
58. A (–5, 0), х = –4, 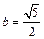 . .
| 59. A (–5, 0), х = –1, 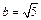 . .
|
60. A (–4, 0), x = –3, 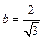 . .
|
В задачах 61–70 систему уравнений записать в матричной форме и решить её с помощью обратной матрицы.
61. 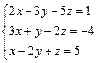
| 62. 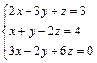
|
63. 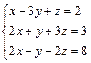
| 64. 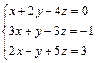
|
65. 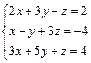
| 66. 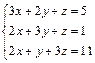
|
67. 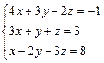
| 68. 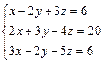
|
69. 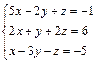
| 70. 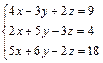
|
В задачах 71–80 решить систему линейных уравнений методом Крамера
71. 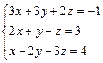
| 72. 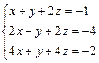
|
73. 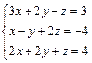
| 74. 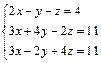
|
75. 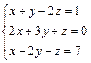
| 76. 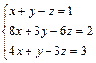
|
77. 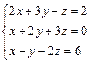
| 78. 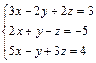
|
79. 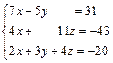
| 80. 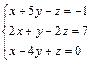
|
В задачах 81–100 исследовать систему линейных уравнений на совместность и решить её, если она совместна.
81. 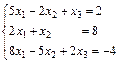
| 82. 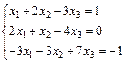
|
83. 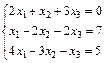
| 84. 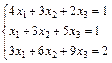
|
85. 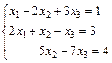
| 86. 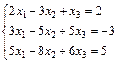
|
87. 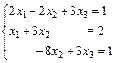
| 88. 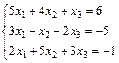
|
89. 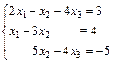
| 90. 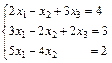
|
91. 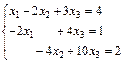
| 92. 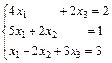
|
93. 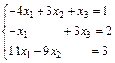
| 94. 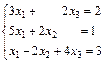
|
95. 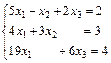
| 96. 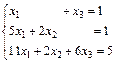
|
97. 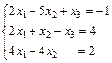
| 98. 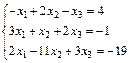
|
99. 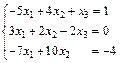
| 100. 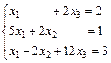
|
 2015-04-30
2015-04-30 965
965








