1. В коробке 15 луковиц гладиолусов, из которых 7 луковиц красных гладиолусов, 8 луковиц черных. Какова вероятность того, что из 10 наудачу выбранных луковиц 6 окажутся луковицами черных гладиолусов?
2. Из 12 луковиц, среди которых 5 луковиц красных тюльпанов и 7 желтых, наудачу выбирают 4. Какова вероятность того, что из них вырастут два красных и два желтых тюльпана?
3. В помете 2 рыжих щенка и 5 черных. Наудачу выбирают трех щенков. Какова вероятность того, что один из них рыжий?
4. Из 12 крыс 8 получили некоторую дозу облучения. Какова вероятность того, что из 6 наудачу выбранных крыс 4 облучены?
5. В популяции из 30 плодовых мушек 10 имеют красные глаза. Наудачу выбирают 5 мушек. Какова вероятность того, что одна из них имеет красные глаза?
6. В 15 пакетиках находится пыльца, собранная с 15 цветков гороха, из которых 5 красных, а остальные – белые. Наудачу выбирают 3 пакетика. Какова вероятность того, что в двух из них пыльца красных цветков?
7. Среди 12 цыплят 5 курочек. Какова вероятность того, что из выбранных наудачу 4 цыплят 2 курочки?
8. Из данных 20 мужчин 1 страдает дальтонизмом. Какова вероятность того, что при случайном выборе 10 мужчин из этих 20 один страдает дальтонизмом?
9. Из колоды в 36 карт выбирают 4 карты. Какова вероятность того, что 3 из них красные?
10. Из 15 вакцинированных мышей у 12 сформировался иммунитет. Какова вероятность того, что из 5 случайно выбранных из группы вакцинированных мышей 4 имеют иммунитет?
11. На ферме из 12 коров 3 больные. Какова вероятность того, что из 4 выбранных наудачу коров 1 больная?
12. Из 15 арбузов 3 неспелых. Какова вероятность того, что из 3 выбранных арбузов 2 спелых?
13. Из 9 лабораторных мышей 7 вакцинированы. Какова вероятность того, что из 5 наудачу выбранных мышей 3 вакцинированы?
14. Среди 10 доноров 4 имеют первую группу крови. Какова вероятность того, что из двух наудачу выбранных доноров один имеет первую группу крови?
15. Среди 15 цветных мышей 10 имеют генотип Сс, а 5 – генотип СС. Какова вероятность того, что из 3 выбранных мышей 2 имеют генотип Сс?
16. В аквариуме из 12 рыбок 4 золотых. Какова вероятность того, что из случайно отловленных 3 рыбок 1 золотая?
17. Среди 10 одинаковых пробирок без этикеток 4 пробирки со штаммом типа «А» и 6 со штаммом типа «В». Какова вероятность того, что из 3 случайно выбранных пробирок 2 со штаммом типа «А»?
18. В питомнике из 10 обезьян 2 имеют отрицательный резус-фактор. Какова вероятность того, что из наудачу выбранных обезьян 1 имеет отрицательный резус-фактор?
19. Среди 6 котят 2 кота. Какова вероятность того, что из двух выбранных наудачу котят 1 кот?
20. Среди 12 мышей 8 короткохвостных. Наудачу выбирают 3 мыши. Какова вероятность того, что 2 из них короткохвостные?
В задачах 21–30 предполагаем, что масса яиц – нормально распределенная случайная величина Х, с математическим ожиданием а и средним квадратическим отклонением s. В заготовку принимают яйца от х1 до х2 граммов. Определить: а) вероятность того, что наудачу взятое яйцо пойдет в заготовку; б)вероятность того, что абсолютная величина отклонения Х-а окажется меньше d; в) по правилу трех сигм найти наибольшую и наименьшую границы предполагаемой массы яйца.
| Номер задачи | а | s | х1 | х2 | d |
В задачах 31–40 Известно, что рост людей, проживающих в данной местности, есть случайная величина Х, распределенная по нормальному закону со средним значением а и средним квадратическим отклонением s. Найти: а) вероятность того, что наудачу выбранный человек имеет рост от х1 до х2 см; б) вероятность того, что абсолютная величина отклонения Х-а окажется меньше d; в) по правилу трех сигм найти наибольшую и наименьшую границы предполагаемого роста человека.
| Номер задачи | а | s | х1 | х2 | d |
В задачах 41–60 задан закон распределения дискретной случайной величины.
Найти:
1) значение параметра а;
2) математическое ожидание М(Х);
3) дисперсию Д(Х).
Построить многоугольник распределения.
| Х | |||||
| р | 0,3 | 0,2 | 0,3 | 0,1 | а |
| Х | |||||
| а | 0,2 | 0,4 | 0,3 | р | 0,1 |
| Х | |||||
| р | 0,2 | 0,1 | 0,5 | 0,1 | а |
| Х | |||||
| р | 0,1 | 0,4 | а | 0,3 | 0,1 |
| Х | |||||
| р | 0,1 | 0,2 | 0,5 | 0,1 | а |
| Х | |||||
| р | 0,1 | 0,4 | 0,2 | 0,1 | а |
| Х | |||||
| р | 0,2 | 0,4 | а | 0,3 | 0,1 |
| Х | |||||
| р | 0,2 | 0,3 | 0,1 | 0,3 | а |
| Х | |||||
| р | 0,2 | 0,3 | а | 0,3 | 0,1 |
| Х | |||||
| р | 0,3 | 0,3 | а | 0,1 | 0,2 |
| Х | |||||
| р | 0,1 | а | 0,1 | 0,2 | 0,1 |
| Х | |||||
| р | 0,1 | 0,1 | а | 0,2 | 0,4 |
| Х | |||||
| р | 0,3 | 0,2 | а | 0,2 | 0,2 |
| Х | |||||
| р | 0,3 | а | 0,1 | 0,2 | 0,2 |
| Х | |||||
| р | 0,5 | а | 0,2 | 0,1 | 0,2 |
| Х | |||||
| р | 0,2 | а | 0,1 | 0,3 | 0,2 |
| Х | |||||
| р | 0,3 | 0,2 | 0,1 | а | 0,2 |
| Х | |||||
| р | а | 0,1 | 0,6 | 0,1 | 0,1 |
| Х | |||||
| р | 0,2 | 0,3 | 0,4 | 0,1 | а |
| Х | |||||
| р | 0,2 | 0,3 | 0,1 | а | 0,4 |
В задачах 61–80 случайная величина Х задана функцией распределения. Требуется:
1) найти функцию плотности вероятности f(x);
2) найти математическое ожидание и дисперсию случайной величины Х;
3) построить графики функций F(x) и f(x).
61. F(x)= 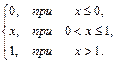
62. F(x)= 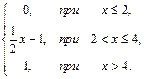
63. F(x)= 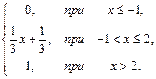
64. F(x)= 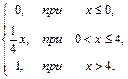
65. F(x)= 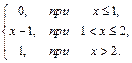
66. F(x)= 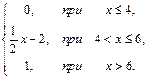
67. F(x)= 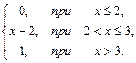
68. F(x)= 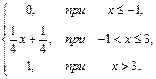
69. F(x)= 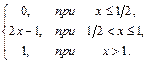
70. F(x)= 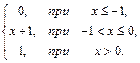
71. F(x)= 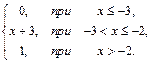
72. F(x)= 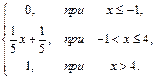
73. F(x)= 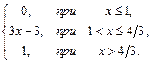
74. F(x)= 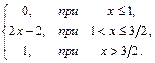
75. F(x)= 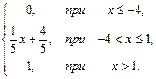
76. F(x)= 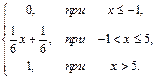
77. F(x)= 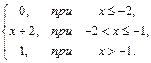
78. F(x)= 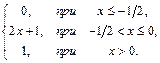
79. F(x)= 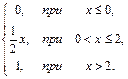
80. F(x)= 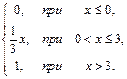
В задачах 81–100 закон распределения двумерной дискретной случайной величины (Х, Y) задан таблицей. Найти:
1) частные законы распределения случайных величин Х и Y;
2) математические ожидания М (Х) и М (Y);
3) дисперсии D (Х) и D (Y);
4) корреляционный момент Cxy;
5) коэффициент корреляции rxy;
6) условный закон распределения случайной величины Х при условии, что случайная величина Y принимает своё наименьшее значение.
| 81. | 82. | |||||||
| Х Y | –1 | Х Y | ||||||
| 0,2 | 0,1 | 0,3 | 0,1 | 0,1 | ||||
| 0,1 | 0,2 | 0,2 | 0,2 | |||||
| 0,1 | 0,2 | 0,2 |
| 83. | 84. | |||||||
| Х Y | –2 | –1 | Х Y | |||||
| 0,1 | 0,2 | 0,1 | –2 | 0,2 | 0,1 | 0,2 | ||
| 0,1 | 0,1 | –1 | 0,1 | 0,1 | ||||
| 0,2 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 |
| 85. | 86. | |||||||
| Х Y | –2 | Х Y | ||||||
| 0,1 | 0,1 | 0,2 | –2 | 0,2 | ||||
| 0,2 | 0,1 | –1 | 0,2 | 0,1 | ||||
| 0,2 | 0,1 | 0,2 | 0,2 | 0,1 |
| 87. | 88. | |||||||
| Х Y | –2 | Х Y | ||||||
| 0,1 | 0,1 | 0,2 | 0,1 | 0,1 | 0,1 | |||
| 0,1 | 0,2 | 0,1 | 0,1 | 0,2 | ||||
| 0,1 | 0,1 | 0,1 | 0,3 |
| 89. | 90. | |||||||
| Х Y | Х Y | –3 | –2 | –1 | ||||
| –2 | 0,1 | –3 | 0,1 | 0,2 | ||||
| –1 | 0,2 | 0,3 | 0,1 | –2 | 0,1 | 0,1 | ||
| 0,1 | 0,1 | 0,1 | –1 | 0,2 | 0,1 | 0,2 |
| 91. | 92. | |||||||
| Х Y | Х Y | |||||||
| –1 | 0,1 | 0,1 | –1 | 0,1 | 0,1 | 0,1 | ||
| 0,2 | 0,2 | 0,1 | 0,2 | 0,2 | 0,2 | |||
| 0,2 | 0,1 | 0,1 |
| 93. | 94. | |||||||
| Х Y | –3 | Х Y | –3 | –2 | ||||
| –1 | 0,1 | 0,2 | 0,1 | 0,2 | 0,2 | |||
| 0,1 | 0,2 | 0,1 | 0,1 | 0,1 | 0,1 | |||
| 0,1 | 0,1 | 0,1 | 0,2 |
| 95. | 96. | |||||||
| Х Y | Х Y | –3 | ||||||
| –2 | 0,1 | 0,1 | 0,1 | 0,2 | 0,1 | |||
| 0,2 | 0,2 | 0,1 | 0,1 | 0,2 | 0,1 | |||
| 0,1 | 0,1 | 0,1 | 0,1 | 0,1 |
| 97. | 98. | |||||||
| Х Y | –3 | Х Y | ||||||
| –1 | 0,1 | 0,1 | 0,1 | –2 | 0,2 | 0,1 | ||
| 0,1 | 0,2 | 0, | –1 | 0,2 | 0,1 | 0,1 | ||
| 0,2 | 0,2 | 0,1 | 0,1 | 0,1 |
| 99. | 100. | |||||||
| Х Y | –1 | Х Y | ||||||
| –1 | 0,1 | 0,1 | 0,1 | 0,2 | 0,1 | 0,1 | ||
| 0,1 | 0,2 | 0,1 | 0,1 | 0,2 | 0,1 | |||
| 0,1 | 0,1 | 0,1 | 0,1 | 0,1 |
Контрольная работа по математике №3
Составители: Бабин Владислав Николаевич
Бильданов Ринат Талгатович
Бурков Сергей Николаевич
Грунина Мария Викторовна
Редактор Н.К.Крупина
Лицензия №020426 от 7 мая 1997 г.
Подписано к печати “__”_______ 201_ г. Формат 84´108/32
Объём 0,8 уч.-изд.л. Тираж 100 экз.
Издательский центр НГАУ
630039, Новосибирск, ул. Добролюбова, 160
 2015-04-30
2015-04-30 2468
2468








