В задачах 261-265 найти частные производные второго порядка 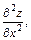
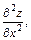
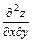 .
.
261. 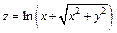 . 262.
. 262. 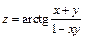 .
.
263. 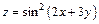 . 264.
. 264. 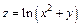 .
.
265. 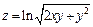 .
.
В задачах 266-270 найти дифференциалы второго порядка от данных функций.
266. 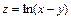 . 267.
. 267. 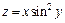 .
.
268. 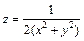 . 269.
. 269. 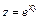 .
.
270. 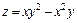 .
.
В задачах 271-275 проверить равенства.
271. 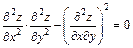 , если
, если 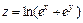 .
.
272. 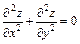 , если
, если 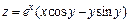 .
.
273. 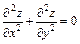 , если
, если 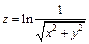 .
.
274. 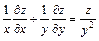 , если
, если 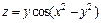 .
.
275. 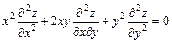 , если
, если 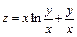 .
.
В задачах 276 – 280 написать уравнения касательных плоскостей и нормалей к данным поверхностям в указанных точках.
276. 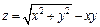 , М(3; 4; –7).
, М(3; 4; –7).
277. 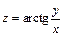 , М(1; 1;
, М(1; 1; 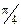 ).
).
278. 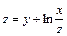 , М(1; 1; 1).
, М(1; 1; 1).
279. 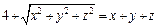 , М(2; 3;6).
, М(2; 3;6).
280. 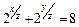 , М(2; 2; 1).
, М(2; 2; 1).
В задачах 281 – 290 исследовать на экстремум функцию 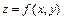 .
.
281. 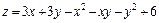 . 282.
. 282. 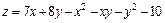 .
.
283. 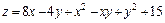 . 284.
. 284. 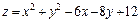 .
.
285. 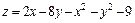 . 286.
. 286. 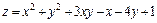 .
.
287. 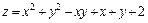 . 288.
. 288. 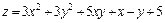 .
.
289. 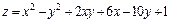 . 290.
. 290. 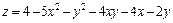 .
.
В задачах 291 – 300 найти наименьшее и наибольшее значение функции 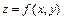 в данной замкнутой области.
в данной замкнутой области.
291. 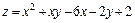 в прямоугольнике 1 ≤ x ≤ 3, 1 ≤ y ≤ 4.
в прямоугольнике 1 ≤ x ≤ 3, 1 ≤ y ≤ 4.
292. 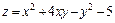 в треугольнике, ограниченном осями Ox и Oy и прямой y = 2 – x.
в треугольнике, ограниченном осями Ox и Oy и прямой y = 2 – x.
293. 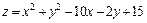 в прямоугольнике 2 ≤ x ≤ 6, 0 ≤ y ≤ 5.
в прямоугольнике 2 ≤ x ≤ 6, 0 ≤ y ≤ 5.
294. 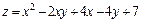 в области, ограниченной параболой
в области, ограниченной параболой 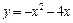 и осью Ox.
и осью Ox.
295. 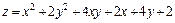 в квадрате 0 ≤ x ≤ 2, 0 ≤ y ≤ 2.
в квадрате 0 ≤ x ≤ 2, 0 ≤ y ≤ 2.
296. 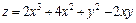 в области, ограниченной параболой
в области, ограниченной параболой 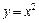 , прямой y = 4 и осью Oy (x ≥ 0).
, прямой y = 4 и осью Oy (x ≥ 0).
297. 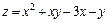 в прямоугольнике 0 ≤ x ≤ 2, 0 ≤ y ≤ 3.
в прямоугольнике 0 ≤ x ≤ 2, 0 ≤ y ≤ 3.
298. 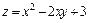 в области, ограниченной параболой y = 4 – x 2 и осью Ox.
в области, ограниченной параболой y = 4 – x 2 и осью Ox.
299. 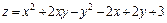 в треугольнике, ограниченном прямыми y = 0, x = 2, y = x + 2.
в треугольнике, ограниченном прямыми y = 0, x = 2, y = x + 2.
300. 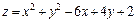 в прямоугольнике 0 ≤ x ≤ 4, –3 ≤ y ≤ 2.
в прямоугольнике 0 ≤ x ≤ 4, –3 ≤ y ≤ 2.
В задачах 301 – 310 построить на плоскости Oxy область интегрирования заданного интеграла; изменить порядок интегрирования и вычислить интеграл.
301. 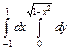 . 302.
. 302. 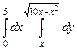 .
.
303. 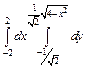 . 304.
. 304. 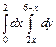 .
.
305. 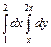 . 306.
. 306. 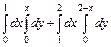 .
.
307. 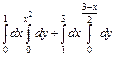 . 308.
. 308. 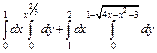 .
.
309. 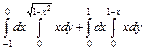 . 310.
. 310. 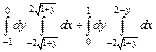 .
.
В задачах 311 – 320 построить на плоскости Oxy область интегрирования; перейти к полярным координатам и вычислить интеграл.
311. 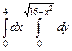 . 312.
. 312. 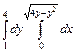 .
.
313. 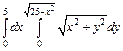 . 314.
. 314. 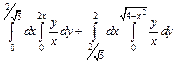 .
.
315. 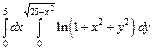 . 316.
. 316. 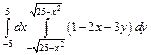 .
.
317. 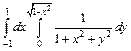 . 318.
. 318. 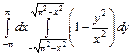 .
.
319. 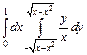 . 320.
. 320. 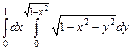 .
.
В задачах 321 – 340 найти объемы тел, ограниченных следующими поверхностями. Данное тело и область интегрирования изобразить на чертеже.
321. 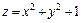 , x = 4, у = 4, x = 0, y = 0, z = 0.
, x = 4, у = 4, x = 0, y = 0, z = 0.
322. 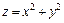 , z = 0, у = 1, у = 2 х, у = 6 – х.
, z = 0, у = 1, у = 2 х, у = 6 – х.
323. 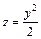 , 2 x + 3 y = 12, x = 0, y = 0, z = 0.
, 2 x + 3 y = 12, x = 0, y = 0, z = 0.
324. 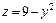 , 3 x + 4 y = 12, x = 0, у = 0, z = 0.
, 3 x + 4 y = 12, x = 0, у = 0, z = 0.
325. 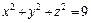 ,
, 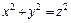 , z ≥ 0.
, z ≥ 0.
326. 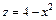 ,
, 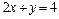 , x = 0, у = 0, z = 0
, x = 0, у = 0, z = 0
327. 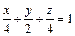 ,
, 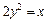 , z = 0.
, z = 0.
328. 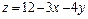 ,
, 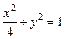 , z = 0.
, z = 0.
329. 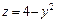 ,
, 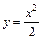 , z = 0.
, z = 0.
330. 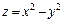 , x = 3, z = 0.
, x = 3, z = 0.
331. 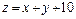 ,
, 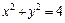 , z = 0.
, z = 0.
332. 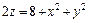 ,
, 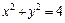 , z = 0.
, z = 0.
333. 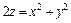 ,
, 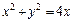 , z = 0.
, z = 0.
334. 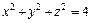 ,
, 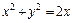 , z ≥ 0.
, z ≥ 0.
335. 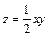 ,
, 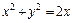 , z = 0, x ≥ 0, y ≥ 0.
, z = 0, x ≥ 0, y ≥ 0.
336. 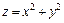 , x + y = l, x = 0, y = 0, z = 0.
, x + y = l, x = 0, y = 0, z = 0.
337. 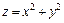 ,
, 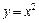 , у = 1, z = 0.
, у = 1, z = 0.
338. 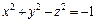 ,
, 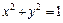 , z = 0.
, z = 0.
339. 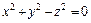 ,
, 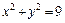 , z ≥ 0.
, z ≥ 0.
340. 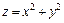 , z = x + y.
, z = x + y.
В задачах 341 – 360 найти работу силы 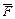 при перемещении вдоль линии L от точки M к точке N.
при перемещении вдоль линии L от точки M к точке N.
341. 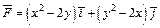 , L: отрезок MN, М (–4, 0), N (0, 2).
, L: отрезок MN, М (–4, 0), N (0, 2).
342. 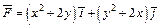 , L:отрезок MN, M (–4, 0), N (0, 2).
, L:отрезок MN, M (–4, 0), N (0, 2).
343. 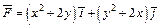 , L:
, L: 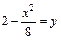 , M (–4, 0), N (0, 2).
, M (–4, 0), N (0, 2).
344. 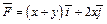 , L:
, L: 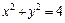 (у ≥ 0), M (2, 0), N (–2, 0).
(у ≥ 0), M (2, 0), N (–2, 0).
345. 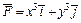 , L:
, L: 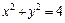 (x ≥ 0, у ≥ 0), M (2, 0), N (0, 2).
(x ≥ 0, у ≥ 0), M (2, 0), N (0, 2).
346. 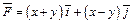 , L:
, L: 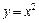 , M (–l, 1), N (1, 1).
, M (–l, 1), N (1, 1).
347. 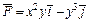 , L:отрезок MN, M (–1, 0), N (0, 1).
, L:отрезок MN, M (–1, 0), N (0, 1).
348. 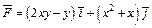 , L:
, L: 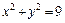 (y ≥ 0), M (3, 0), N (–3, 0).
(y ≥ 0), M (3, 0), N (–3, 0).
349. 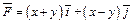 , L:
, L: 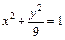 (x ≥ 0, y ≥ 0), M (1, 0), N (0, 3).
(x ≥ 0, y ≥ 0), M (1, 0), N (0, 3).
350. 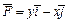 , L:
, L: 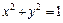 (y ≥ 0), M (l, 0), N (–1, 0).
(y ≥ 0), M (l, 0), N (–1, 0).
351. 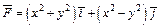 , L:
, L: 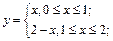 M (2, 0), N (0, 0).
M (2, 0), N (0, 0).
352. 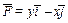 , L:
, L: 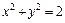 (x ≥ 0, y ≥ 0),
(x ≥ 0, y ≥ 0), 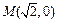 ,
, 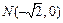 .
.
353. 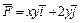 , L:
, L: 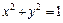 (x ≥ 0, y ≥ 0), M (1, 0), N (0, 1).
(x ≥ 0, y ≥ 0), M (1, 0), N (0, 1).
354. 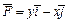 , L:
, L: 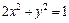 (y ≥ 0),
(y ≥ 0), 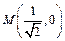 ,
, 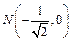 .
.
355. 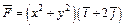 , L:
, L: 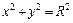 (y ≥ 0), M (R, 0), N (– R, 0).
(y ≥ 0), M (R, 0), N (– R, 0).
356. 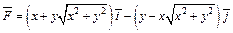 , L:
, L: 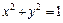 (y ≥ 0), M (1, 0), N (–1,0).
(y ≥ 0), M (1, 0), N (–1,0).
357. 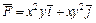 , L:
, L: 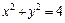 (x ≥ 0, y ≥ 0), M (2, 0), N (0, 2).
(x ≥ 0, y ≥ 0), M (2, 0), N (0, 2).
358. 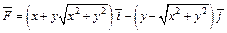 , L:
, L: 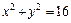 (x ≥ 0, y ≥ 0), M (4, 0), N (0, 4).
(x ≥ 0, y ≥ 0), M (4, 0), N (0, 4).
359. 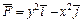 , L:
, L: 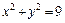 (x ≥ 0, y ≥ 0), M (3, 0), N (0, 3).
(x ≥ 0, y ≥ 0), M (3, 0), N (0, 3).
360. 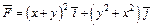 , L: отрезок MN, M (1, 0), N (0, 1).
, L: отрезок MN, M (1, 0), N (0, 1).
 2015-04-30
2015-04-30 686
686








