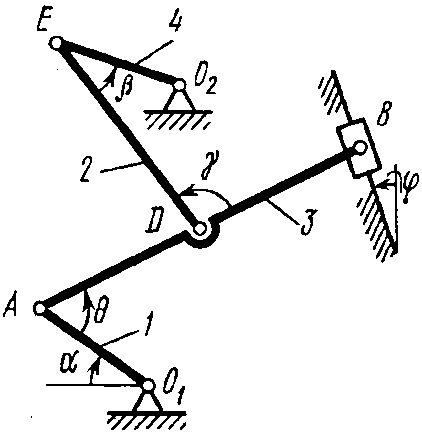
 Механизм (рис. К2,а) состоит из стержней 1, 2, 3, 4 и ползуна
Механизм (рис. К2,а) состоит из стержней 1, 2, 3, 4 и ползуна 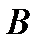 , соединенных друг с другом и с неподвижными опорами
, соединенных друг с другом и с неподвижными опорами 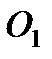 и
и 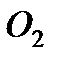 шарнирами.
шарнирами.
| Рис. К2,а |
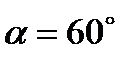 ,
, 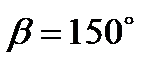 ,
, 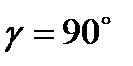 ,
, 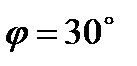 ,
, 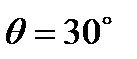 ,
, 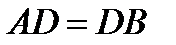 ,
, 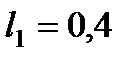 м,
м, 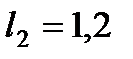 м,
м, 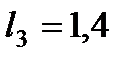 м,
м, 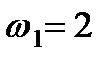 с-1,
с-1, 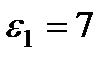 с-2 (направления
с-2 (направления 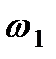 и
и 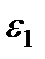 – против хода часовой стрелки).
– против хода часовой стрелки).
Определить: 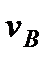 ,
, 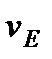 ,
, 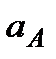 ,
, 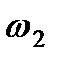 .
.
Решение:
1. Строим положение механизма в соответствии с заданными углами и выбранным масштабом длин (рис. К2,б; на этом рисунке изображаем все векторы скоростей).
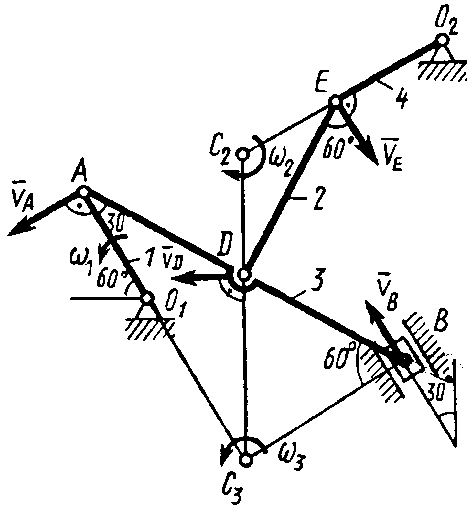 2. Определяем
2. Определяем 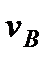 . Точка
. Точка 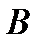 принадлежит стержню
принадлежит стержню 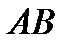 . Чтобы найти
. Чтобы найти 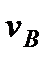 , надо знать скорость какой-нибудь другой точки этого стержня и направление
, надо знать скорость какой-нибудь другой точки этого стержня и направление 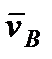 . По данным задачи, учитывая направление
. По данным задачи, учитывая направление 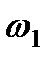 , можем определить
, можем определить 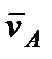 . Численно:
. Численно:
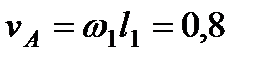 м/с,
м/с,
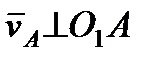 . (1)
. (1)
| Рис. К2,б |
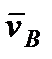 найдем, учтя, что точка
найдем, учтя, что точка 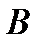 принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная
принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная 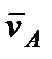 и направление
и направление 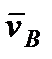 , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня 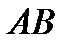 ) на прямую, соединяющую эти точки (прямая
) на прямую, соединяющую эти точки (прямая 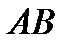 ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 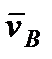 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
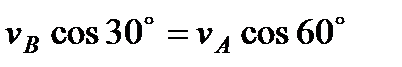 ,
, 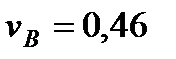 м/с. (2)
м/с. (2)
3. Определяем 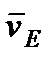 . Точка
. Точка 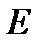 принадлежит стержню
принадлежит стержню 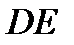 . Следовательно, по аналогии с предыдущим, чтобы определить
. Следовательно, по аналогии с предыдущим, чтобы определить 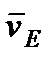 , надо сначала найти скорость точки
, надо сначала найти скорость точки 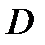 , принадлежащей одновременно стержню
, принадлежащей одновременно стержню 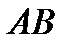 . Для этого, зная
. Для этого, зная 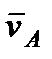 и
и 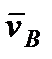 , строим мгновенный центр скоростей (МЦС) стержня
, строим мгновенный центр скоростей (МЦС) стержня 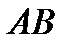 . Это точка
. Это точка 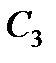 , лежащая на пересечении перпендикуляров к
, лежащая на пересечении перпендикуляров к 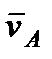 и
и 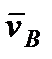 , восставленных из точек
, восставленных из точек 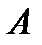 и
и 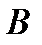 (к
(к 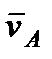 перпендикулярен стержень 1). По направлению вектора
перпендикулярен стержень 1). По направлению вектора 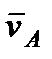 определяем направление поворота стержня
определяем направление поворота стержня 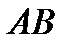 вокруг МЦС
вокруг МЦС 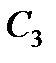 . Вектор
. Вектор 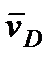 перпендикулярен отрезку
перпендикулярен отрезку 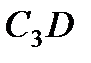 , соединяющему точки
, соединяющему точки 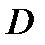 и
и 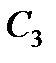 , и направлен в сторону поворота. Величину
, и направлен в сторону поворота. Величину 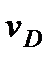 найдем из пропорции:
найдем из пропорции:
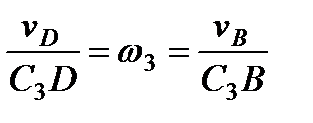 . (3)
. (3)
Чтобы вычислить 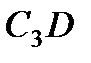 и
и 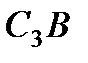 , заметим, что
, заметим, что 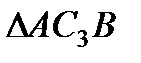 – прямоугольный, так как острые углы в нем равны 30° и 60°, и что
– прямоугольный, так как острые углы в нем равны 30° и 60°, и что 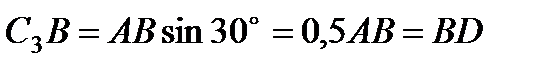 . Тогда
. Тогда 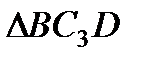 является равносторонним и
является равносторонним и 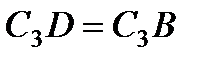 . В результате равенство (3) дает
. В результате равенство (3) дает
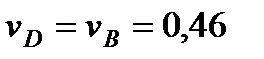 м/с,
м/с, 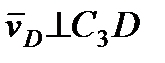 . (4)
. (4)
Так как точка 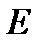 принадлежит одновременно стержню
принадлежит одновременно стержню 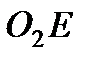 , вращающемуся вокруг
, вращающемуся вокруг 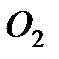 , то
, то 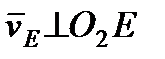 . Тогда, восставляя из точек
. Тогда, восставляя из точек 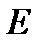 и
и 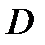 перпендикуляры к скоростям
перпендикуляры к скоростям 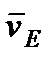 и
и 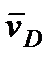 , построим МЦС
, построим МЦС 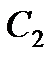 стержня
стержня 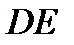 . По направлению вектора
. По направлению вектора 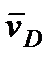 определяем направление поворота стержня
определяем направление поворота стержня 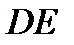 вокруг центра
вокруг центра 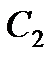 . Вектор
. Вектор 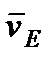 направлен в сторону поворота этого стержня. Из рис. К2,б видно, что
направлен в сторону поворота этого стержня. Из рис. К2,б видно, что 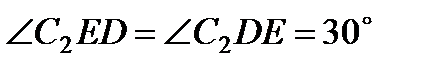 , откуда
, откуда 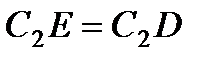 . Составив теперь пропорцию, найдем, что
. Составив теперь пропорцию, найдем, что
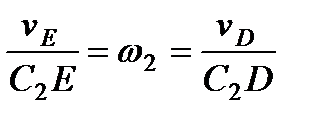 ,
, 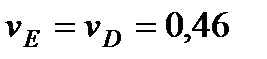 м/с. (5)
м/с. (5)
4. Определяем 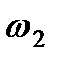 . Так как МЦС стержня 2 известен (точка
. Так как МЦС стержня 2 известен (точка 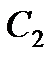 ) и
) и 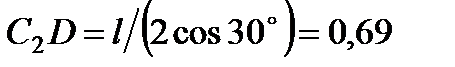 м, то
м, то
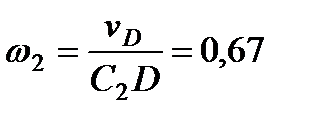 с–1. (6)
с–1. (6)
5. Определяем 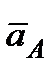 (рис. К2,в, на котором изображаем все
(рис. К2,в, на котором изображаем все 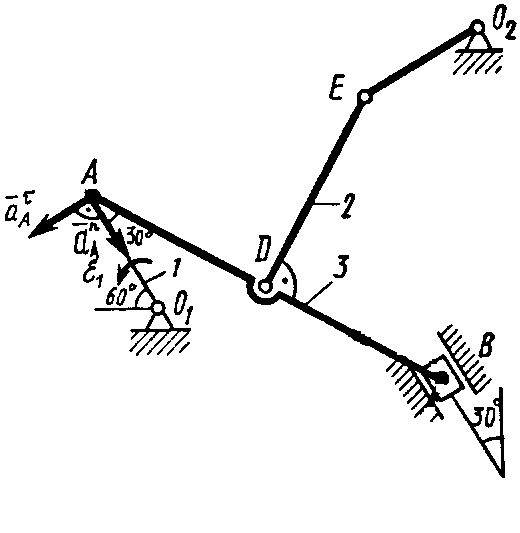 векторы ускорений). Точка
векторы ускорений). Точка 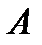 принадлежит стержню 1. Полное ускорение точки
принадлежит стержню 1. Полное ускорение точки 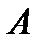 разложим на тангенциальную и нормальную составляющие:
разложим на тангенциальную и нормальную составляющие:
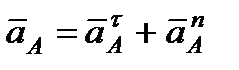 ,
,
где численно
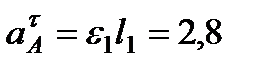 м/с2,
м/с2,
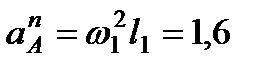 м/с2. (7)
м/с2. (7)
| Рис. К2,в |
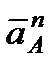 направлен вдоль
направлен вдоль 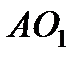 , а
, а 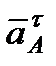 – перпендикулярно
– перпендикулярно 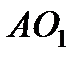 . Изображаем эти векторы на чертеже (см. рис. К2в). Вычисляем
. Изображаем эти векторы на чертеже (см. рис. К2в). Вычисляем
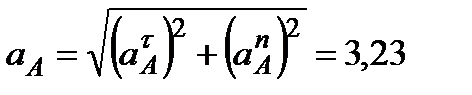 м/с2.
м/с2.
Ответ: 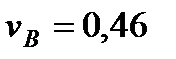 м/с,
м/с, 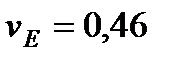 м/с,
м/с, 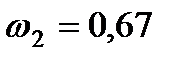 с–1,
с–1, 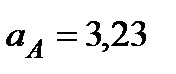 м/с2.
м/с2.
КОНТРОЛЬНЫЕ ВОПРОСЫ
 2015-04-30
2015-04-30 410
410








