Даны уравнения движения точки в плоскости 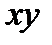 :
:
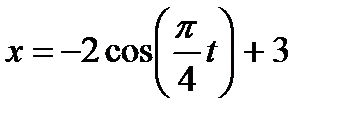 ,
, 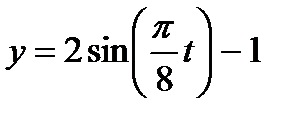
(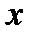 ,
, 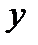 – в сантиметрах,
– в сантиметрах, 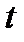 – в секундах).
– в секундах).
Определить уравнение траектории точки; для момента времени 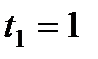 с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Решение:
1. Для определения уравнения траектории точки исключим из заданных уравнений движения время 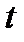 . Поскольку
. Поскольку 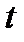 входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
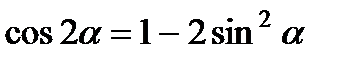 :
:
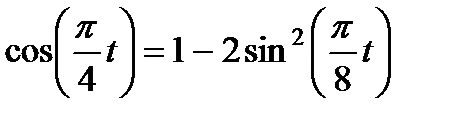 . (1)
. (1)
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим
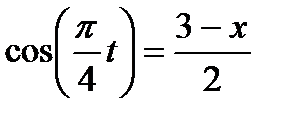 ,
, 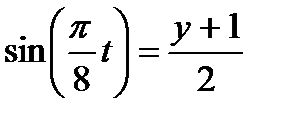 ,
,
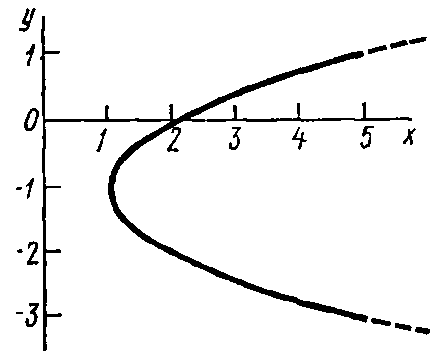 следовательно,
следовательно,
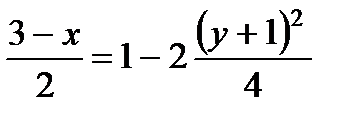 .
.
Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. К1,а):
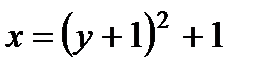 . (2)
. (2)
| Рис. К1,а |
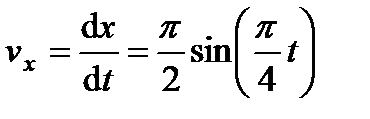 ,
, 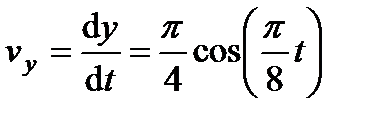 ,
,
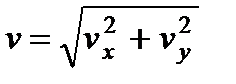 .
.
Для момента времени 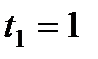 с:
с: 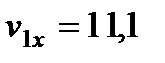
 ,
, 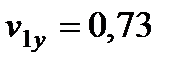
 ,
, 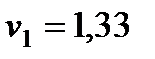
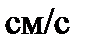 .
.
3. Аналогично найдем ускорение точки:
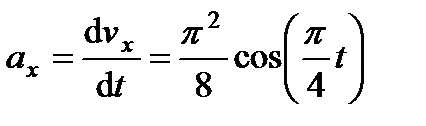 ,
, 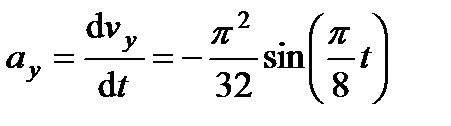 ,
,
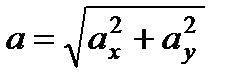 .
.
Для момента времени 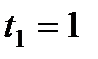 с:
с: 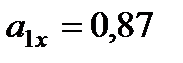
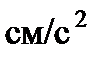 ,
, 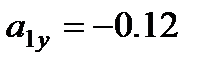
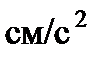 ,
, 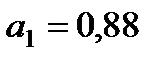
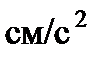 . (4)
. (4)
4. Касательное ускорение найдем, дифференцируя по времени равенство:
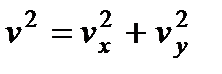
Получим
 ,
,
откуда
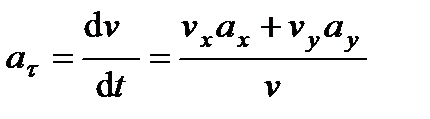 . (5)
. (5)
Числовые значения всех величин, входящих в правую часть выражения (5), определены и даются равенствами (3) и,(4). Подставив в (5) эти числа, найдем сразу, что при 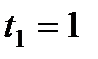 с:
с: 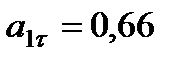
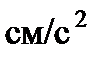 .
.
5. Нормальное ускорение точки 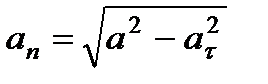 . Подставляя сюда найденные при
. Подставляя сюда найденные при 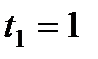 с числовые значения
с числовые значения 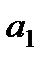 и
и 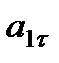 , получим, что
, получим, что 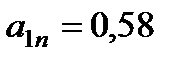
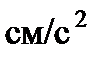 .
.
6. Радиус кривизны траектории 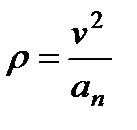 . Подставляя сюда числовые значения
. Подставляя сюда числовые значения 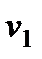 и
и 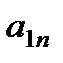 при
при 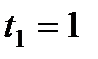 с, найдем, что
с, найдем, что 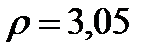 см.
см.
Ответ: 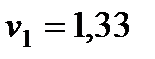
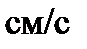 ,
, 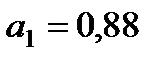
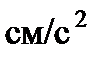 ,
, 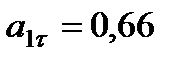
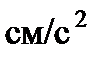 ,
, 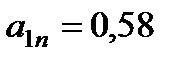
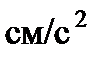 ,
, 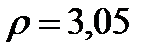 см.
см.
 2015-04-30
2015-04-30 349
349








