Молекулалық физиканың көптеген құбылыстарын қарастырғанда атом ішіндегі процестердің кванттық сипаты ғана емес, сонымен қатар атом құрылымы да ескерілмейді. Біз массасы мен көлемі аз көптеген молекулалардан тұратын жүйелерді қарастырамыз. Мұндай жүйелерді теориялық тұрғыда қарастыру өте күрделі. Себебі, ол үшін барлық молекулалардың бір-бірімен әсерлесу күштерін ескеру қажет. Егер молекулалардың қозғалысын механика заңдарына бағынады деп есептесек, онда кез келген молекулалық жүйені толық сипаттау үшін берілген күштер әсерімен барлық молекулалардың қозғалысы туралы механикалық есепті шығару керек. Демек, саны жүйедегі молекулалар санынан үш есе көп қозғалыс теңдеулерін жазып шешу керек. Егер 1см3 көлемде қалыпты жағдайда 2,7•1019 молекула болатынын ескерсек, онда мұндай теңдеулер санын жазудың өзі көп уақыт алады. Молекулалар санының көптігі әрбір молекуланың қозғалысын жеке-жеке қарастырудың керек еместігін көрсетеді. Бөлшектер саны осындай көп болғанда, олардың қозғалысын сипаттайтын физикалық шамалардың (жылдамдық, энергия,...) орташа мәнімен шектелуге болады. Молекулалық жүйелерді қарастырғанда осы әдісті қолданамыз.
Заттардың агрегаттық үш күйінің ішінде газ тәріздес күй ең қарапайым. Себебі газ молекулалары арасындағы күштер өте әлсіз және көптеген жағдайларда әсерлесу күштері ескерілмейді. Молекулалық физика курсында молекулалар арасындағы күштер тіптен жоқ, молекулалардың өлшемдері де елеусіз, демек материялық нүктелер деп қарастырылады. Мұндай жуықтаулар газ молекулаларының еркін екенін көрсетеді. Демек, олар түзу сызықты бірқалыпты қозғалады. Әрбір молекула ыдыс ішінде өзінен басқа молекулалар жоқ сияқты қозғалады.
Бір-бірімен әсерлеспейтін материялық нүктелер жүйесі ретінде қарастырылатын газдар – идеал газ деп аталады. Сонымен, идеал газға мынадай қасиеттер тән болуы керек:
- молекулалардың өлшемдері елеусіз материялық нүктелер ретінде қарастырылады;
- молекулалар бір-бірімен әсерлеспейді;
- молекулалар түзу сызықты бірқалыпты қозғалыста болады.
Бақылау сұрақтары:
1. Заттардың агрегаттық күйлерін атаңыз және олардың негізгі қасиеттерін көрсетіңіз.
2. Идеал газдың анықтамасын тұжырымдаңыз.
3. Идеал газға тән негізгі қасиеттерді атаңыз.
§5. Газ қысымы. Молекула-кинетикалық теорияның негізгі теңдеуі
1. Газ қысымы. Молекулалардың қозғалысын қарастырғанда біз олардың газ ішіндегі кез келген дене бетімен, ыдыс қабырғаларымен соқтығысуларын және олардың бір-бірімен соқтығысуларын ескеруіміз керек. Молекулалар бей-берекет қозғалыс кезінде ыдыс қабырғаларына немесе газ ішіндегі дене беттеріне өте жақын келеді. Сондай-ақ, олар бір-біріне де өте аз арақашықтыққа жақындайды. Бұл жағдайда газ молекулалары басқа молекулалармен арасындағы арақашықтық артқан сайын тез азаятын әсерлесу күштері пайда болады. Осы күштердің әсерінен газ молекулалары өз қозғалыстарының бағытын өзгертеді. Бұл процесс соқтығысу деп аталады.
Молекулалардың өзара соқтығысуы өте маңызды. Қазір біз молекулалардың ыдыс қабырғасымен соқтығысуларын қарастырамыз. Себебі, осы әсерлесулер ыдыс қабырғаларының газ молекулалары тарапынан алатын күшін анықтайды. Әрине бұл күш қабырғалар ауданы неғұрлым көп болса, соғұрлым көп болады. Молекулалардың қабырғаға әсерін қабырға ауданына тәуелді күшпен емес – қысым арқылы сипаттаған ыңғайлы:
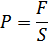
Газдың ыдыс қабырғаларына қысым түсіруі – газдардың негізгі қасиеттерінің бірі. Газдың бар екендігін осы қысымның болуымен анықтауға болады. Сондықтан газ қысымы – газды негізгі сипаттаушы шамалардың бірі болып табылады. Ыдыс қабырғаларына газдың қысым түсіруі – газ молекулаларының ыдыс қабырғасымен ретсіз, көптеген соқтығысуларының салдары екенін XVIII ғасырда Даниил Бернулли байқаған. Молекулалардың қабырғаны соғулары ыдыс қабырғаларының деформациясына әкеледі. Сондықтан ыдыс қабырғасы да газға серпімді әсер етеді.
2. Молекула-кинетикалық теорияның негізгі теңдеуі. Параллелепипед пішінді ыдыстағы тепе-теңдік күйдегі газды қарастырайық. Демек, кез-келген бағытта қозғалған молекулалар саны кері бағытта қозғалған молекулалар санына тең болсын. Осы ыдыстың abcd қабырғасына түсірілетін газ қысымын анықтайық.Молекулалар жылдамдығы қалай бағытталса да біз оның х осіне проекциясын қарастырамыз (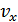 ). Ойша газдың
). Ойша газдың 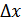 қабатын қарастырайық. Оған серпімді деформацияланған қабырға тарапынан
қабатын қарастырайық. Оған серпімді деформацияланған қабырға тарапынан 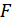 күшіәсер етеді. Абсолюттік мәні тура сондай күшпен газ да қабырғаға әсер етеді. Ньютонның 2-ші заңы бойынша күш импульсі
күшіәсер етеді. Абсолюттік мәні тура сондай күшпен газ да қабырғаға әсер етеді. Ньютонның 2-ші заңы бойынша күш импульсі 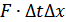 –газ қабатының импульсінің өзгерісіне тең. Осы қабатқа
–газ қабатының импульсінің өзгерісіне тең. Осы қабатқа 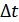 уақыт ішінде енетін молекулалар санын анықтайық. a/b/c/d/ - шекарасына
уақыт ішінде енетін молекулалар санын анықтайық. a/b/c/d/ - шекарасына 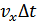 арақашықтағы молекулалар енсін. Демек, көлемі
арақашықтағы молекулалар енсін. Демек, көлемі 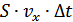 болатын параллелепипед ішіндегі молекулаларенетін болсын. Егер көлем бірлігінде n -молекула болса, онда
болатын параллелепипед ішіндегі молекулаларенетін болсын. Егер көлем бірлігінде n -молекула болса, онда 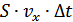 көлемде
көлемде 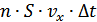 молекула болады. Бірақ, осы молекулалардың жартысы ғана оңға қарай қозғалады, демек,
молекула болады. Бірақ, осы молекулалардың жартысы ғана оңға қарай қозғалады, демек, 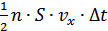 . Сонымен,
. Сонымен, 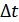 уақыт ішінде қабатқа солдан оңға қарай
уақыт ішінде қабатқа солдан оңға қарай 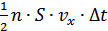 молекула енеді. Молекулалардың әрқайсысының импульсі
молекула енеді. Молекулалардың әрқайсысының импульсі 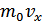 , онда a/b/c/d/ шекарасына енетін барлық молекулалардың толық импульсі
, онда a/b/c/d/ шекарасына енетін барлық молекулалардың толық импульсі
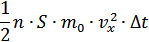
Осы 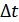 уақыт ішінде бұл қабаттан осыншама молекула оңнан солға қарай шығады. Сонымен қабаттан шығатын теріс импульспен қабатқа кіретін оң импульсті ескерсек, онда қабаттағы импульстің өзгерісі былай анықталады:
уақыт ішінде бұл қабаттан осыншама молекула оңнан солға қарай шығады. Сонымен қабаттан шығатын теріс импульспен қабатқа кіретін оң импульсті ескерсек, онда қабаттағы импульстің өзгерісі былай анықталады:
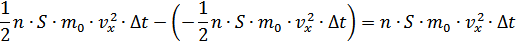
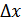 -қабаттың импульсінің осы өзгерісі
-қабаттың импульсінің осы өзгерісі 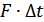 күш импульсімен теңеседі:
күш импульсімен теңеседі:
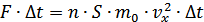
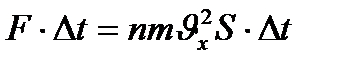
Осы өрнектің екі жағында 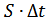 -көбейтіндісіне бөліп қысымныңөрнегін анықтаймыз:
-көбейтіндісіне бөліп қысымныңөрнегін анықтаймыз:
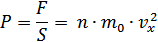
Енді 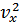 шамасын, осы шаманың орташа мәнімен ауыстырамыз
шамасын, осы шаманың орташа мәнімен ауыстырамыз 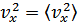 , онда қысым үшін анықталған өрнекті мына түрде көрсете аламыз:
, онда қысым үшін анықталған өрнекті мына түрде көрсете аламыз:
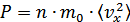
Әрбір молекуланың 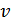 -жылдамдығы үшін мына өрнек орындалады:
-жылдамдығы үшін мына өрнек орындалады:
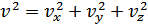 .
.
Сондықтан
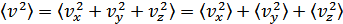
Молекулалардың қозғалысы бей-берекет болғандықтан
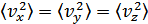 . Демек
. Демек 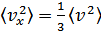 . Осыларды ескерсек, онда МКТ-ның негізгі теңдеуінің (қысымның) өрнегі мына түрге келеді:
. Осыларды ескерсек, онда МКТ-ның негізгі теңдеуінің (қысымның) өрнегі мына түрге келеді:
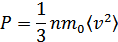
немесе
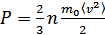 ,
,
мұндағы 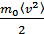 - бір молекуланың орташа кинетикалық энергиясы. Сонымен, молекула-кинетикалық теорияның негізгі теңдеуін мына түрде жаза аламыз:
- бір молекуланың орташа кинетикалық энергиясы. Сонымен, молекула-кинетикалық теорияның негізгі теңдеуін мына түрде жаза аламыз:
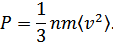
Егер 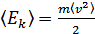 екендігін ескерсек, онда МКТ-ның негізгі теңдеуін мына түрде жазуға болады:
екендігін ескерсек, онда МКТ-ның негізгі теңдеуін мына түрде жазуға болады:
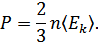
Сонымен, көлем бірлігіндегі газ қысымы молекулалардың орташа кинетикалық энергиясының 2/3-бөлігіне тең.
3. Молекулалардың энергиясы мен температура арасындағы қатынас. Қарастырылып отырған газдың идеал газ екендігін ескерейік, демек молекулалар материалдық нүкте ретінде қарастырылады. Мұндай молекулалардың кинетикалық энергиясы тек қана молекуланың ілгерілемелі қозғалысымен анықталады. Идеал газ үшін оның температурасы кинетикалық энергияның 2/3 бөлігіне тура пропорционал деп ескеру қысым өрнегін ықшамды түрге келтіреді:
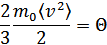
Мұндағы 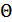 -бір молекулаға тиісті энергия, демек температураға тәуелді функция болып табылады. Енді қысымның өрнегін мына түрде жазамыз:
-бір молекулаға тиісті энергия, демек температураға тәуелді функция болып табылады. Енді қысымның өрнегін мына түрде жазамыз:
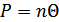
Температура градуспен өлшенетіндіктен, 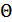 - функциясы температурамен тура пропорционал болу үшін сәйкес пропорционалдық коэффициентін енгізу керек. Ол коэффициентті k -әрпімен белгілейміз. Онда орташа кинетикалық энергиямен температура арасындағы байланыс мына түрде жазылады:
- функциясы температурамен тура пропорционал болу үшін сәйкес пропорционалдық коэффициентін енгізу керек. Ол коэффициентті k -әрпімен белгілейміз. Онда орташа кинетикалық энергиямен температура арасындағы байланыс мына түрде жазылады:
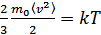 ,
,
бұдан
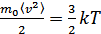 .
.
Молекуланың ілгерілемелі қозғалысының жылдамдығын x,y және z бағыттарына жіктеуге болады. Демек, әр бағытқа энергияның 1/3 бөлігі сәйкес келеді, онда бір бағытқа сәйкес келетін энергия
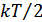 шамасына тең болады.
шамасына тең болады.
Энергия мен температура арасындағы қатынасты сипаттайтын k- коэффициенті Больцман тұрақтысы деп аталады. Әрине, бұл коэффициент экспериментте анықталуы тиіс. Бұл тұрақты маңызды болғандықтан оны әртүрлі әдістермен анықтаған және оның қазіргі кезде қабылданған дәл мәні бірліктердің Халықаралық жүйесінде (ХЖ) мынадай:
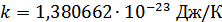
Соңғы формулаға сәйкес температураның мәні нөлге тең болғанда молекулалардың бей-берекет қозғалысының орташа кинетикалық энергиясы да нөлге тең болады. Нөлдік температурада молекулалардың ілгерілемелі қозғалысы тоқтайды. Демек, бұл абсолюттік температура шкаласының санақ басына сәйкес келетін абсолюттік нөл болып табылады.
Соңғы формуланы ескерсек, онда молекула-кинетикалық теорияның негізгі теңдеуін мына түрде жаза аламыз:
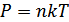
4. Қысым бірлігі. Бірліктердің халықаралық жүйесіндеқысым бірлігі ретінде 1 м2аудан бірлігіне түсірілген шамасы 1 Ньютон күш алынған. Демек, қысым бірлігі 1Н/м2. Бұл бірлікті Блез Паскальдің құрметіне Паскаль (Па) деп атау келісілген.
1 Па=1Н/м2
Бақылау сұрақтары:
1. Қысымның анықтамасын тұжырымдаңыз.
2. Молекула-кинетикалық теорияның негізгі теңдеуін тұжырымдаңыз.
3. Орташа кинетикалық энергия қалай анықталады?
4. Абсолюттік нөл температурада ілгерілемелі қозғалыстың кинетикалық энергиясы қандай мәнге ие болады?
5. Бірліктердің халықаралық жүйесіндегі қысым бірлігі?
§6. Идеал газ күйінің теңдеуі
Молекула-кинетикалық көзқарас негізінде алынған теңдеулер газ күйін сипаттауға болатын физикалық шамалардың өзара қатынасын анықтауға мүмкіндік береді. Мұндай шамалар: P – қысым, Т – температура және V – көлем. Оларды газ күйінің параметрлері деп атайды. Осы үш шама бір-біріне тәуелді. Олардың әрқайсысы қалған екеуінің функциясы болып табылады. Осы үш параметрлерді байланыстыратын (P,V,Т) (газдың тұрақты массасы үшін) теңдеуді газ күйінің теңдеуі деп атайды.
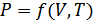 (6.1)
(6.1)
Бұдан газ күйі екі параметрмен анықталатындығы көрінеді. Үшінші параметр алдыңғы екеуімен анықталады.
Идеал газдар үшін күй теңдеуін МКТ-ның негізгі теңдеуінен (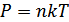 )шығаруға болады.Егер V көлемде N бөлшек болса, онда молекулалар концентрациясы
)шығаруға болады.Егер V көлемде N бөлшек болса, онда молекулалар концентрациясы 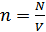 болып анықталады. Онда, МКТ-ның негізгі теңдеуі мына түрде жазылады:
болып анықталады. Онда, МКТ-ның негізгі теңдеуі мына түрде жазылады:
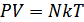 (6.2)
(6.2)
Соңғы теңдеуде газ күйінің үш параметрі бір-бірімен байланысқан, сондықтан оны күй теңдеуі ретінде қарастыруға болады. Мұндағы анықталуы қиынға соғатын молекулалар санын газ массасы мен мольдік масса (М) арқылы өрнектеген дұрыс:
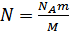 ,
,
мұндағы 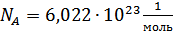 Авогадро тұрақтысы деп аталады. Кез келген заттың бір моліндегі бөлшектер саны Авогадро тұрақтысына тең. Осыны ескеріп идеал газ күйінің теңдеуін мына түрде жазамыз:
Авогадро тұрақтысы деп аталады. Кез келген заттың бір моліндегі бөлшектер саны Авогадро тұрақтысына тең. Осыны ескеріп идеал газ күйінің теңдеуін мына түрде жазамыз:
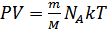 .
.
Авогадро мен Больцман тұрақтыларының көбейтіндісі универсал газ тұрақтысы деп аталады:
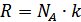 , (6.3)
, (6.3)
мұндағы R – универсал газ тұрақтысы
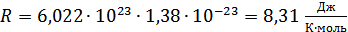 .
.
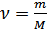 - мольдер саны. Егер
- мольдер саны. Егер 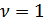 , демек газдың бір молі үшінидеал газ күйінің теңдеуі мына түрде жазылады:
, демек газдың бір молі үшінидеал газ күйінің теңдеуі мына түрде жазылады:
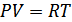 . (6.4)
. (6.4)
Ал, кез келген мольдер саны үшін идеал газ күйініңтеңдеуін мына түрде жаза аламыз:
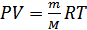 , (6.5)
, (6.5)
немесе
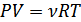 . (6.6)
. (6.6)
Осы түрде жазылған идеал газ күйінің теңдеуін Менделеев-Клапейронтеңдеуі деп атайды.
Бақылау сұрақтары:
1. Газ күйін сипаттайтын қандай макропараметрлерді білесіз?
2. Молекулалар концентрациясы қалай анықталады?
3. Газдың бір молінде қанша молекула болады?
4. Идеал газ күйінің теңдеуін тұжырымдаңыз.
§7. Идеал газ заңдары
1. Бойль-Мариотт заңы. Құрамы мен массасы тұрақты болып қалатын идеал газды тұрақты температура кезінде қарастырайық. Тұрақты температурада газ күйінің өзгеру процесі изотермиялық процесс деп аталады. Егер Менделеев-Клапейрон теңдеуінде T=const болса, онда
| P |
| V |
| T1 |
| T2 |
| T3 |
| 0 |
| 4-сурет. Изотермалар. |
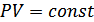 (7.1)
(7.1)
Бұл теңдеу изотермиялық процесстің теңдеуі болып табылады. Бойль-Мариотт заңына сәйкес газдың берілген массасы үшін тұрақты температура кезінде оның қысымы мен көлемінің көбейтіндісі тұрақты болып қалады. Әр түрлі температуралар үшін қысымның көлемге тәуелділігі изотермалар деп аталады. Изотермалар – гиперболалар болып табылады. 4-суретте массасы тұрақты идеал газдың әртүрлі температураларына сәйкес келетін изотермалар көрсетілген. Мұндағы температуралардың қатынасы мынадай 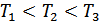 , демек PV диаграммасында температурасы жоғары изотерма жоғарырақ жатады.
, демек PV диаграммасында температурасы жоғары изотерма жоғарырақ жатады.
| 5-сурет. |
| V |
| T |
| P1 |
| P2 |
| P3 |
| 0 |
| 6-сурет. Изобарлар. |
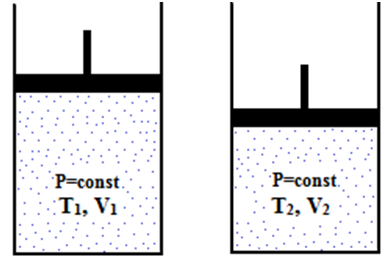
2. Гей-Люссак заңы. Енді массасы мен құрамы өзгермейтігн идеал газдың P қысымы тұрақты болып қалып, оның температурасы мен көлемі өзгеретін болсын. Мұндай шартты орындау үшін газды жылжымалы поршенмен жабылған цилиндрде ұстайық (5-сурет). Мұндай цилиндрдегі газдың температурасын өзгерткен кезде газдың қысымы өзгеріп, ол поршенді жылжытады да, газдың көлемі де өзгереді. Газ тепе-теңдік күйіне келген кезде газ қысымы бастапқы мәнін қабылдайды.
Менделеев-Клапейрон теңдеуінде қысым тұрақты болса 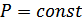 , онда көлемнің температураға қатынасы тұрақты болады
, онда көлемнің температураға қатынасы тұрақты болады 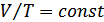 . Демек,
. Демек,
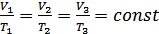 . (7.2)
. (7.2)
Бұл процесс изобаралық процесс деп аталады. Егер температура абсолюттік шкала бойынша алынса, онда изобаралық процестің графигі – изобаралар координаттар басынан шығатын түзу болып табылады (6-сурет).
| P |
| T |
| V1 |
| V2 |
| V3 |
| 0 |
| 7-сурет. Изохоралар. |
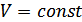 ,онда қысым мен температураның бір-біріне тәуелділігі мынандай заңдылықпен өзгереді:
,онда қысым мен температураның бір-біріне тәуелділігі мынандай заңдылықпен өзгереді: 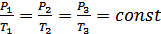 . (7.3)
. (7.3)
Демек,
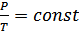 .
.
Егер температура абсолюттік шкала бойынша алынса, онда изохоралық процестің графигі – изохоралар координаттар басынан шығатын түзу болып табылады (7-сурет).
4. Авогадро заңы. Бұл заң бойынша: бірдей қысым, бірдей температура кезінде газдың бірдей көлемінде молекулалардың бірдей саны болады. Осы заңнан керісінше, түрліше газдардың молекулаларының бірдей санының бірдей температура мен бірдей қысым кезінде бірдей көлем қабылдайтындығы шығады. Сондықтан, газдың 1 молі берілген қысым мен температура кезінде бірдей көлем қабылдайды. Мысалы, 00С температурада, 1,01•105Па қысымда газдың 1 молінің көлемі:
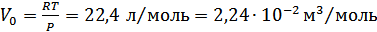 . (7.4)
. (7.4)
Осы қалыпты жағдайда 1м3 көлемдегі молекулалар саны Лошмидт саны деп аталады:
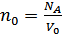 . (7.5)
. (7.5)
Егер Авогадро санымен мольдік көлем мәндерін осы формулаға қойсақ, онда Лошмидт санының мәні 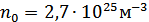 болады.
болады.
5. Дальтон заңы. Көлемі бірдей V болатын ыдыстардың ішінде әртүрлі газдар болсын. Газдардың сол ыдыста тұрғандағы қысымдары сәйкесінше 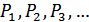 болсын.Егер осы бірдей ыдыстардағы газдарды бір ылыс ішінде араластырып жібергеннен кейін жүйе тепе-теңдік күйге келетін болса және олардың арасында ешқандай реакциялар жүрмесе, онда қоспаның қысымы былай анықталады:
болсын.Егер осы бірдей ыдыстардағы газдарды бір ылыс ішінде араластырып жібергеннен кейін жүйе тепе-теңдік күйге келетін болса және олардың арасында ешқандай реакциялар жүрмесе, онда қоспаның қысымы былай анықталады:
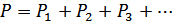 (7.6)
(7.6)
мұндағы 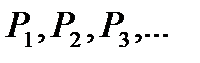 - парциалдық қысымдар. Парциалдық қысым деп, қоспадағы бір газ сол ыдыстың көлемін тек қана жалғыз өзі алып тұрғандағы қысымды айтамыз. Сонымен, қоспа газдың қысымы парциал қысымдардың қосындысына тең болады. Бұл заңды ең алғаш эмпирикалық жолмен Дальтон анықтаған.
- парциалдық қысымдар. Парциалдық қысым деп, қоспадағы бір газ сол ыдыстың көлемін тек қана жалғыз өзі алып тұрғандағы қысымды айтамыз. Сонымен, қоспа газдың қысымы парциал қысымдардың қосындысына тең болады. Бұл заңды ең алғаш эмпирикалық жолмен Дальтон анықтаған.
Дальтон заңын идеал газдың күй теңдеуінен де шығаруға болады. Ол үшін күй теңдеуін мына түрде жазайық:
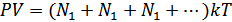 ,
, 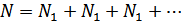
Бұдан
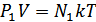 ,
, 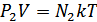 ,
, 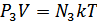 , ….
, ….
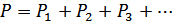 .
.
Бақылау сұрақтары:
1. Изопроцесстер орындалуы үшін қандай алғы шарттар орындалуы керек?
2. Егер «тұрақты температурада» газ көлемін өте жылдам өзгертетін болсақ, изотермиялық процесс орындала ма?
3. Изотермалар қандай қисықпен сипатталады?
4. Қалыпты жағдайдағы газдың 1 молінің көлемі қандай?
5. Лошмидт саны қалай анықталады?
6. Қандай қысымды парциал қысым деп атайды?
§8. Орташа квадраттық жылдамдық
1. 5-параграфта қысым үшін қорытылып шығарылған формулалар газ молекулаларыныңжылулық қозғалыстарының жылдамдықтары туралы айтуға мүмкіндік береді. Газдағы барлық молекулалар бірдей жылдамдықтармен қозғалмайды. Газ ішінде өте баяу молекулалармен қатар жылдамдықтары орташа жылдамдықтан бірнеше есе үлкен молекулалар да кездеседі. Енді газ молекулаларының орташа квадраттық жылдамдығын қарастырайық. Орташа квадраттық жылдамдық былай анықталады:
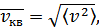
яғни молекулалардың ілгерілемелі қозғалысының жылдамдықтарының квадраттарының орташа мәнінің квадраттық түбірі болады. Орташа квадраттық жылдамдықты анықтау үшін мына түрдегі 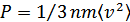 қысым формуласын қарастырайық:
қысым формуласын қарастырайық:
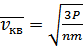 .
.
Бұдан 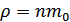 ,
, 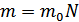 екендігін ескерсек, онда орташа квадраттық теңдеуді мына түрде жаза аламыз:
екендігін ескерсек, онда орташа квадраттық теңдеуді мына түрде жаза аламыз:
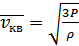 (8.1)
(8.1)
Газ тығыздығын былай 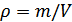 өрнектеп, орташа квадраттық жылдамдықты Менделеев-Клапейрон теңдеуін қолданып жазааламыз:
өрнектеп, орташа квадраттық жылдамдықты Менделеев-Клапейрон теңдеуін қолданып жазааламыз:
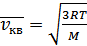 .
.
Осы формуланы қолданып кейбір газдардың молекулаларының орташа квадраттық жылдамдықтарын есептеп көрейік. Мысалы, 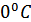 (273.15 K) температурадағы молекулалық сутегі газының молекулаларының орташа квадраттық жылдамдығын анықтайық. Сутегі молекуласының мольдік массасы
(273.15 K) температурадағы молекулалық сутегі газының молекулаларының орташа квадраттық жылдамдығын анықтайық. Сутегі молекуласының мольдік массасы 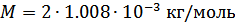 .
.
 .
.
Осы жолмен азот молекулаларының орташа квадраттық жылдамдығын 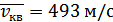 және оттегі үшін
және оттегі үшін 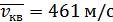 екендігін анықтауға болады.
екендігін анықтауға болады.
2. Штерн тәжірибесі. Молекулалар және атомдар шоғымен жасалған тәжірибелерде де олардың жылдамдығының мәні шамамен
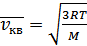 -формуласымен есептегендей шығады. Жоғары вакуумдағы молекулалар бір-бірімен соғтығыспайды деп есептеуге болады, олар тек ыдыстың қабырғаларымен соқтығысады. Осыны пайдаланып молекулалар мен атомдар шоғын алуға болады. Молекулалар мен атомдар шоғын жоғары вакуумде металдарды немесе басқа заттарды қыздыру арқылы алады. Шоғырдағы атомдардың жылдамдығын тікелей өлшеуді ең алғаш 1920 жылы О.Штерн іске асырды. Оның классикалық саналатын тәжірибесінің қарапайым сызбасы 8–суретте көрсетілген. Сыртынан күмістің жұқа қабаты жағылған А платина қыл сым С цилиндрдің өсі бойымен орналасқан. Цилиндр ішіндегі ауа шамасы
-формуласымен есептегендей шығады. Жоғары вакуумдағы молекулалар бір-бірімен соғтығыспайды деп есептеуге болады, олар тек ыдыстың қабырғаларымен соқтығысады. Осыны пайдаланып молекулалар мен атомдар шоғын алуға болады. Молекулалар мен атомдар шоғын жоғары вакуумде металдарды немесе басқа заттарды қыздыру арқылы алады. Шоғырдағы атомдардың жылдамдығын тікелей өлшеуді ең алғаш 1920 жылы О.Штерн іске асырды. Оның классикалық саналатын тәжірибесінің қарапайым сызбасы 8–суретте көрсетілген. Сыртынан күмістің жұқа қабаты жағылған А платина қыл сым С цилиндрдің өсі бойымен орналасқан. Цилиндр ішіндегі ауа шамасы 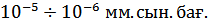 қысымға вакуумдық сорғышпен үнемі сорылып отырған. Қылсым бойымен электр тогы өткенде, ол күмістің балқу температурасынан (961,9 ºС) жоғары температураға дейін қызады. Жоғары температураға дейін қызған күміс интенсивті буланып, оның атомдары түзу сызықты бірқалыпты А қыл сымынан С цилиндрдің ішкі бетіне қарай ұшқан. Күміс атомдары цилиндр бетінде жақсы конденсирленуі үшін цилиндр суытылды. Ұшқан атомдардың жолында жіңішке саңлауы бар В экран қойылды. Атомдар шоғы цилиндрдің ішкі бетіне орнатылған қабылдаушы пластинаға конденсирленді. Цилиндрді және онымен бірге экранмен қылсымды 2500÷2700 мин-1жиілігімен айналдыруға болады. Осы жүйе тыныштықта болғанда күміс атомдары В саңлауынан өтеді және қабылдаушы пластина бетінде конденсирленіп оның бетінде В саңлауының
қысымға вакуумдық сорғышпен үнемі сорылып отырған. Қылсым бойымен электр тогы өткенде, ол күмістің балқу температурасынан (961,9 ºС) жоғары температураға дейін қызады. Жоғары температураға дейін қызған күміс интенсивті буланып, оның атомдары түзу сызықты бірқалыпты А қыл сымынан С цилиндрдің ішкі бетіне қарай ұшқан. Күміс атомдары цилиндр бетінде жақсы конденсирленуі үшін цилиндр суытылды. Ұшқан атомдардың жолында жіңішке саңлауы бар В экран қойылды. Атомдар шоғы цилиндрдің ішкі бетіне орнатылған қабылдаушы пластинаға конденсирленді. Цилиндрді және онымен бірге экранмен қылсымды 2500÷2700 мин-1жиілігімен айналдыруға болады. Осы жүйе тыныштықта болғанда күміс атомдары В саңлауынан өтеді және қабылдаушы пластина бетінде конденсирленіп оның бетінде В саңлауының
| А |
| В |
| С |
| D |
| D/ |
| 8-сурет. Штерн тәжірибесі. |
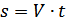 формуласымен анықталады, мұнда
формуласымен анықталады, мұнда 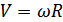 -айналған цилиндр бетінің нүктелерінің сызықтық жылдамдығы, R -оның радиусы,
-айналған цилиндр бетінің нүктелерінің сызықтық жылдамдығы, R -оның радиусы, 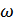 -бұрыштық жылдамдығы, t – шамасы күміс атомдарының BD-арақашықтығын өту уақыты. Бұл арақашықтықты l -әріпімен белгілесек, онда
-бұрыштық жылдамдығы, t – шамасы күміс атомдарының BD-арақашықтығын өту уақыты. Бұл арақашықтықты l -әріпімен белгілесек, онда 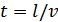 , мұнда
, мұнда 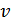 -күміс атомдарының жылдамдығы. Сонымен,
-күміс атомдарының жылдамдығы. Сонымен, 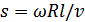 , бұдан күміс атомдарының жылдамдығын мына түрде анықтаймыз:
, бұдан күміс атомдарының жылдамдығын мына түрде анықтаймыз: 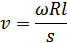
Штерннің тәжірибелерінде Dкескіні үнемі айқын, ал D/ кескіні көмескілеу болған. Бұл факт күміс атомдарының жылдамдықтары әртүрлі болғанын көрсетеді. Бұл тәжірибеде қыл сымның температурасы шамамен 1200 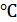 болған. Күміс атомдарының жылдамдықтарының
болған. Күміс атомдарының жылдамдықтарының 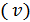 мәндері 560÷640 м/с аралығында, демек (8.1) теңдеумен күміс атомдары үшінесептелген орташа квадрат жылдамдық мәніне (584 м/с) өте жақсы жуықтайды. Сонымен, Штерн тәжірибесінің нәтижелері молекула-кинетикалық теориямен сапалық деңгейде үйлеседі.
мәндері 560÷640 м/с аралығында, демек (8.1) теңдеумен күміс атомдары үшінесептелген орташа квадрат жылдамдық мәніне (584 м/с) өте жақсы жуықтайды. Сонымен, Штерн тәжірибесінің нәтижелері молекула-кинетикалық теориямен сапалық деңгейде үйлеседі.
Бақылау сұрақтары:
1. Орташа квадраттық жылдамдық қалай анықталады?
2. Идеал газ күйінің теңдеуін қолданып орташа квадрат жылдамдықты анықтаңыз.
3. Штерн тәжірибесін сипаттап беріңіз.
 2015-04-30
2015-04-30 4050
4050
