Метод предназначен для выделения одного или подмножества наиболее предпочтительных объектов. Характерными особенностями метода являются:
a) наличие процедуры формирования "идеального" объекта (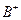 ), служащего своего рода целью, к которой надо стремиться. Такой "идеал", как правило, недостижим и не существует реально, но его полезно иметь для понимания ЛПР своих целей;
), служащего своего рода целью, к которой надо стремиться. Такой "идеал", как правило, недостижим и не существует реально, но его полезно иметь для понимания ЛПР своих целей;
b) на каждой итерации производится исключение объектов, не претендующих на наиболее предпочтительные, т.е. не выделяются "лучшие" объекты, а исключаются "худшие".
В общем виде алгоритм метода следующий. Сначала исключаются доминируемые объекты, так как среди них не может быть наиболее предпочтительного.
Формируется "идеальный" объект 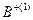 из наиболее предпочтительных значений критериев и "антиидеальный" из наименее предпочтительных значений. Определяются расстояния от объектов из исходного множества до "антиидеала", на основании которых выделяются "худшие" объекты. Среди таких объектов, как правило, есть объекты, имеющие одно наиболее предпочтительное
из наиболее предпочтительных значений критериев и "антиидеальный" из наименее предпочтительных значений. Определяются расстояния от объектов из исходного множества до "антиидеала", на основании которых выделяются "худшие" объекты. Среди таких объектов, как правило, есть объекты, имеющие одно наиболее предпочтительное  значение (объекты
значение (объекты 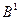 и
и 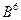 на рис 2.2).
на рис 2.2).
После исключения "худших" объектов вновь переходим к этапу формирования "идеала", и он изменяется, приближаясь к реальным объектам (на рисунке это 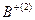 ).
).
Процедура заканчивается, когда останется небольшое число объектов, которые и считаютсянаиболее предпочтительными.
|
После выбора наиболее предпочтительного объекта у ЛПР возникает неудовлетворенность, вызванная тем фактом, что выбран именно данный объект, а не другой. Такую неудовлетворенность называют конфликтом после решения.
На первых итерациях метода превалирует конфликт перед решением. На последующих итерациях "идеал" приближается к реальным объектам, и конфликт перед решением уменьшается. Однако конфликт после решения может увеличиваться. Это свидетельствует о недостаточной изученности ЛПР решаемой задачи.
Рассмотрим подробно алгоритм метода на примере выбора организации для работы.
Пусть исходное множество организаций включает  =8 объектов. В качестве критериев используем следующие три: k1 – уровень заработной платы (тыс. руб. в месяц), k2 – удаленность (минут проезда до места работы) k3 – перспектива роста (в баллах от 0 до 10). Ниже представлены 8 организаций с значениями критериев:
=8 объектов. В качестве критериев используем следующие три: k1 – уровень заработной платы (тыс. руб. в месяц), k2 – удаленность (минут проезда до места работы) k3 – перспектива роста (в баллах от 0 до 10). Ниже представлены 8 организаций с значениями критериев:
| Название объекта | Зар. Плата | Удаленность | Перспективы |
| Вариант 1 | |||
| Вариант 2 | |||
| Вариант 3 | |||
| Вариант 4 | |||
| Вариант 5 | |||
| Вариант 6 | |||
| Вариант 7 | |||
| Вариант 8 |
Сначала проанализируем множество вариантов и исключим доминируемые. Среди 8-ми вариантов шестой вариант является доминируемым по отношению к варианту 3, поэтому шестой вариант исключаем.
Этап 1. Формирование "идеального объекта 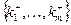 , где
, где 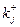 – максимальное по предпочтению значение критерия среди всех объектов, т.е.
– максимальное по предпочтению значение критерия среди всех объектов, т.е.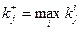 , если предпочтение объекта возрастает при увеличении
, если предпочтение объекта возрастает при увеличении 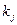 , или
, или 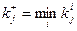 , если предпочтение объекта возрастает при уменьшении критерия.
, если предпочтение объекта возрастает при уменьшении критерия.
Если "идеал" принадлежит множеству объектов, то он и будет наиболее предпочтительным. Но так как МКЗ обычно решается на множестве эффективных объектов, то "идеальный" объект не будет принадлежать исходному множеству.
Наэтом же этапе формируется "антиидеальный" объект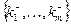 из наименее предпочтительных значений.
из наименее предпочтительных значений.
В рассматриваемом примере «идеальный» и "антиидеальный" объекты:
| Критерий | Идеальный объект | Антиидеальный объект |
| Зар. Плата | ||
| Удаленность | ||
| Перспективы |
Этап 2. Переход от физических единиц измерения критериев к относительным единицам в соответствии с выражением:
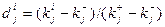 . (2.1)
. (2.1)
В относительных единицах все критерии будут изменяться в интервале 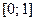 , при этом, чем меньше
, при этом, чем меньше 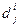 , тем ближе объект по критерию
, тем ближе объект по критерию 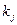 к "антиидеальному".
к "антиидеальному".
| Название объекта | Зар. Плата | Удаленность | Перспективы |
| Вариант 1 | 0,25 | 0,8 | 0,2 |
| Вариант 2 | 0,4 | ||
| Вариант 3 | 0,875 | 0,4 | 0,2 |
| Вариант 4 | 0,5 | 0,6 | |
| Вариант 5 | 0,6 | ||
| Вариант 7 | 0,2 | ||
| Вариант 8 | 0,625 | 0,4 | 0,8 |
Первые два этапа выполняются автоматически без участия ЛПР.
Этап 3. Задание весов критериев (коэффициентов относительной важности). ЛПР, исходя из своих суждений о важности критериев, задаёт веса критериев 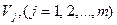 . Пусть V1 = 0.4; V2 = 0.3; V3 = 0.3.
. Пусть V1 = 0.4; V2 = 0.3; V3 = 0.3.
Этап 4. Рассчет расстояния объектов до "антиидеала". В качестве метрики используется следующее выражение:
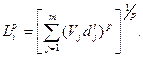
Используя разные 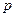 , можно получить различные метрики. Так, при
, можно получить различные метрики. Так, при 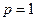 получим аддитивный оператор, а при
получим аддитивный оператор, а при 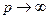 (2.2)переходит в
(2.2)переходит в 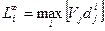 . Чем больше значение
. Чем больше значение 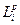 , тем дальше объект от "антиидеала" и ближе к "идеальному". На следующем, пятом, этапе, задавая различные значения p, определяются разные метрики для сравнения с "идеальным". Рассчитаем метрики
, тем дальше объект от "антиидеала" и ближе к "идеальному". На следующем, пятом, этапе, задавая различные значения p, определяются разные метрики для сравнения с "идеальным". Рассчитаем метрики
| p=3 | p=2 | p=1 | p=0,3 | |
| В1 | 0,247 | 0,267 | 0,40 | 4,62 |
| В2 | 0,306 | 0,323 | 0,42 | 1,97 |
| В3 | 0,355 | 0,375 | 0,53 | 5,74 |
| В4 | 0,344 | 0,403 | 0,68 | 8,67 |
| В5 | 0,412 | 0,439 | 0,58 | 2,77 |
| В7 | 0,400 | 0,404 | 0,46 | 1,78 |
| В8 | 0,315 | 0,367 | 0,61 | 7,65 |
Этап 4. Исключение «бесперспективных» вариантов. Для этого при каждом 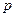 , т.е. для каждой метрики все объекты упорядочиваются по близости к "идеалу" по величине
, т.е. для каждой метрики все объекты упорядочиваются по близости к "идеалу" по величине 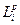 . В результате получим следующую матрицу:
. В результате получим следующую матрицу:
| p=3 | p=2 | p=1 | p=0,3 | Сумма p | |
| Вариант 4 | |||||
| Вариант 5 | |||||
| Вариант 8 | |||||
| Вариант 3 | |||||
| Вариант 7 | |||||
| Вариант 2 | |||||
| Вариант 1 |
В этой матрице варианты упорядочены по значению суммы р, полученной сложением по строке рангов вариантов.
ЛПР принимает решение об исключении объектов, не претендующих на наиболее предпочтительный. Очевидно, что это те объекты, которые при различных метриках (разных p) находятся в конце упорядоченных рядов. Действительно, если независимо от выбранной метрики объект далек от "идеала", то есть все основания исключить его.
Видим, что варианты 1 и 2 по большинству р находятся на последних местах, т.е. он наиболее далеки от идеального объекта и значит, не претендуют на наилучший вариант. Поэтому исключаем варианты 1 и 2.
Снова переходим к первому этапу – формирования идеального и антиидеального объектов.
| Критерий | Идеальный объект | Антиидеальный объект |
| Зар. Плата | ||
| Удаленность | ||
| Перспективы |
Видим, что характеристики идеального и антиидеального объектов изменились, они сместились.
Заново пересчитаем матрицу 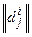 , а затем значения метрик
, а затем значения метрик 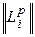 , получим следующую матрицу
, получим следующую матрицу
| p=3 | p=2 | p=1 | p=0,3 | Сумма p | |
| Вариант 4 | |||||
| Вариант 5 | |||||
| Вариант 3 | |||||
| Вариант 7 | |||||
| Вариант 8 |
Обратите внимание порядок вариантов изменился из-за того, что характеристики идеального и антиидеального объектов изменились.
Исключаем Вариант 8 и вновь выполняем этапы 1, 2, 4,5 получаем
| p=4 | p=2 | p=1 | p=0,3 | Сумма p | |
| Вариант 4 | |||||
| Вариант 5 | |||||
| Вариант 3 | |||||
| Вариант 7 |
Исключаем вариант 7
| p=3 | p=2 | p=1 | p=0,3 | Сумма p | |
| Вариант 4 | |||||
| Вариант 5 | |||||
| Вариант 3 |
Из оставшихся надо рассматривать в качестве наиболее предпочтительных варианты 4 и 5.
В заключение отметим, что данный метод наиболее эффективен при больших размерностях задачи.
 2014-02-02
2014-02-02 3117
3117
