Задание 2. Вычислить указанные неопределённые интегралы

Вычислить указанные неопределённые интегралы.

Решение:

а)

.

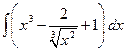По правилам интегрирования:

,

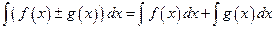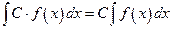, где .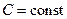

По таблицам интегралов:

.

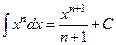Вычисляем заданный интеграл:

.

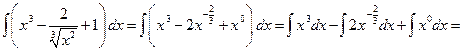
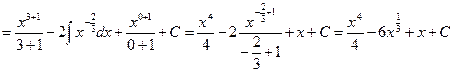б)

.

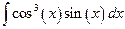По таблицам интегралов:

, .

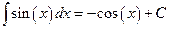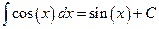Воспользуемся методом замены переменной:

.

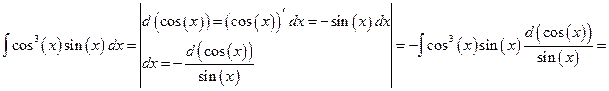
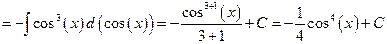в)

.

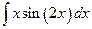Воспользуемся методом интегрирования по частям:

.

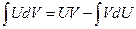Вычисляем заданный интеграл:

.

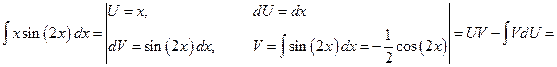
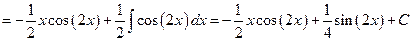Задание 3

Вычислить площадь фигуры, ограниченной линиям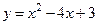и и 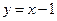. Сделать чертёж.

Определим точки пересечения линий:

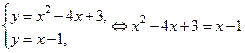, откуда

,

,

, .

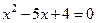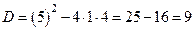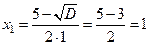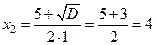Выполним чертеж линий на отрезке 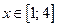, рис. 2.

Площадь фигуры можно определить через интеграл:

.

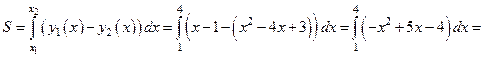
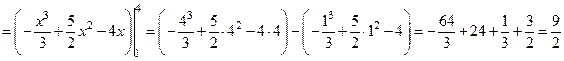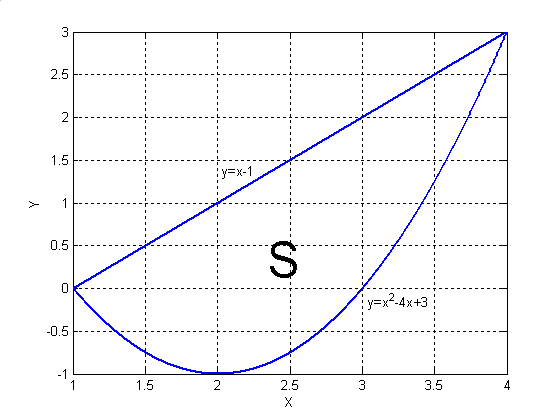
Рис. 2.