Задание 1. Исследовать данную функцию методами дифференциального исчисления и построить её график

Исследовать данную функцию методами дифференциального исчисления и построить её график:

.

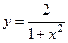Решение:

1. Область определения функции .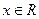

2. Исследуем поведение функции на концах области определения и в точках разрыва (которых нет).

, .

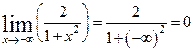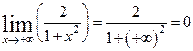Точек разрыва нет.

3. Найдём точки пересечения графика функции с осями координат.

При : .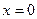

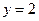При 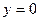получаем уравнение 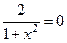, что невозможно, т.е. .

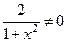Т.о. функция пересекает оси координат в точке .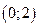

4 Функция не периодична.

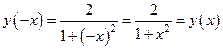, т.е. функция четная, следовательно, симметрична относительно оси ординат.

5 Исследуем функцию на возрастание, убывание и экстремумы.

Находим производную и приравниваем нулю:

.

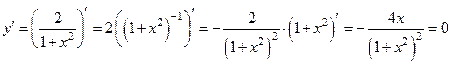Откуда 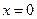, следовательно, рассматриваем только точку .

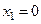На интервале 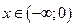значение 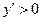, следовательно, функция возрастает. На интервале 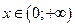значение 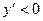, функция убывает.

При переходе через точку 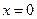производная меняет знак с плюса на минус и, следовательно, эта точка является точкой максимума функции. Значение функции в этой точке равно .

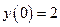6 Исследуем функцию на выпуклость, вогнутость и точки перегиба.

Находим вторую производную и приравниваем нулю:

.

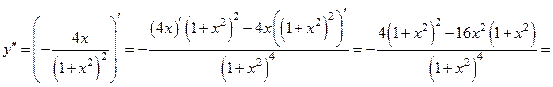
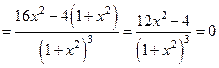Откуда 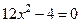, следовательно, рассматриваем точки , .

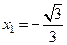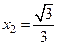При 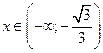значение 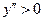, т.е. выпуклость направлена вниз. При 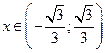значение 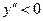, т.е. выпуклость направлена вверх. При 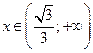значение 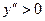, т.е. выпуклость направлена вниз.

При переходе через точки 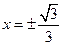значение второй производной меняет знак, следовательно, эти точки являются точками перегиба. Значения функции в этих точках равны: .

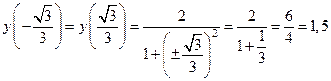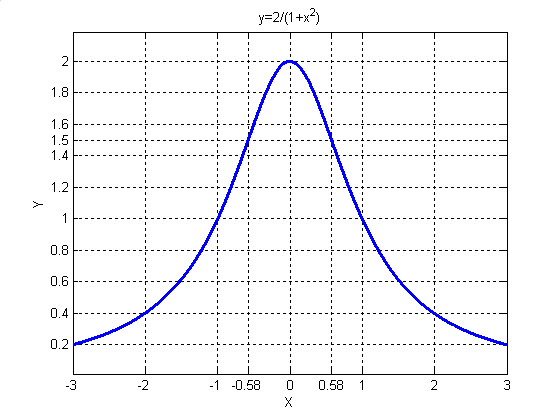
Рис. 1.

7 Определим асимптоты функции.

Точек разрыва нет, следовательно, нет и вертикальных асимптот.

Найдём наклонные асимптоты .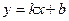

Определим угловой коэффициент наклонной асимптоты:

.

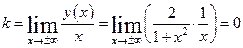Тогда 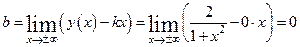. Т.о. прямая 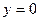– асимптота функции.

8 График функции изображён на рис. 1.