Задание 4. Найти экстремум функции 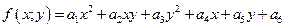, где

Найти экстремум функции , где , , , , , .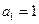

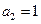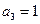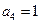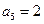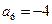Решение:

Запишем исследуемую функцию:

.

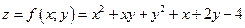Исследуем данную функцию на экстремум.

, .

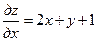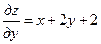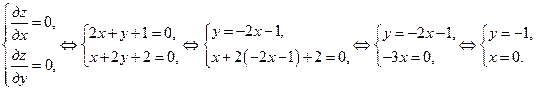
Т.о. точка 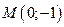является точкой возможного экстремума.

Составим определитель

.

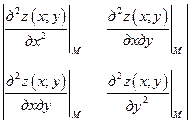Найдём частные производные второго порядка:

, , .

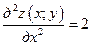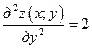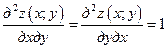Т.к. все частные производные второго порядка постоянные величины, то определитель будет иметь вид:

.

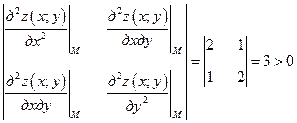Следовательно, точка 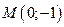является точкой экстремума.

Т.к. 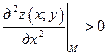и 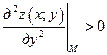, то точка 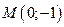является точкой локального минимума.