При определении критичных скоростей в принципе используют метод Данкерли и метод Рейлея.
Метод Рейлея (энергетический метод) заключается в том, что используется закон сохранения энергии.
Предполагается, что в любой момент времени сумма кинетической и потенциальной энергии, накапливаемая системой за счёт динамических деформаций, есть величина постоянная, используется метод наложения.
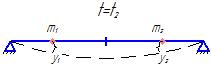
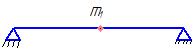
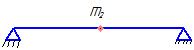
На однопролётный вал закрепляются 2-е массы 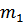 и
и 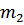 . Предполагается, что в какой-то момент времени под действием динамических нагрузок вал прогибается и получает деформации
. Предполагается, что в какой-то момент времени под действием динамических нагрузок вал прогибается и получает деформации 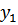 и
и 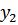 .
.
В этом методе задается величина предполагаемых деформаций «у». В основу метода положено условие, что известно соотношение между деформациями и колеблющимися массами.
В какой-то момент времени 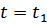 система находится в положении динамического равновесия. Считается, что в этот момент потенциальная энергия U=0.
система находится в положении динамического равновесия. Считается, что в этот момент потенциальная энергия U=0. 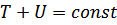 .
.
Т.к. сумма кинетической и потенциальной энергии величина постоянная, то максимальному значению (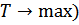 .
.
В какой-то момент времени 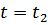 деформации переходят по другую сторону относительно центральной оси вала и в какой-то момент занимают положение равновесия, т.е. все точки системы меняют знак подобно самоцентрированию.
деформации переходят по другую сторону относительно центральной оси вала и в какой-то момент занимают положение равновесия, т.е. все точки системы меняют знак подобно самоцентрированию.
В этом случае в данный момент их скорости равны нулю и T=0, 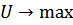
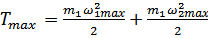 ;
; 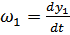 ;
; 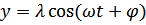 ;
;
При расчётах предполагается, что деформации и потенциальная энергия вырывается через работу внешних сил. За внешние силы принимается момент инерции системы.
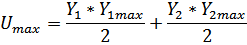
После преобразований: 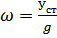 ;
;
Метод Данкерли:
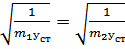 ;
;
После преобразований: 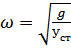 ;
;
На основании приближенных методов Данкерли и Рейлея за основу расчёта критических скоростей берётся скорость: 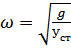 и
и 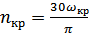 ;
;
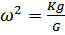 ;
; 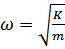 ;
;
 2015-04-30
2015-04-30 603
603








