вариант 1.
15.а) Решите уравнение: sin2x = 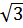 ·cos(
·cos(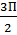 - x).
- x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [ - 3П; - 2П].

| Содержание критерия | Баллы |
| Обоснованно получены верные ответы в обоих пунктах | |
| Обоснованно получен верный ответ в пункте а или в пункте б, ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов – пункта а и пункта б | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
16. В правильной четырёхугольной призме АВСД 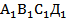 , стороны основания которой равны 3, а боковые рёбра равны 4, найдите угол между прямой А
, стороны основания которой равны 3, а боковые рёбра равны 4, найдите угол между прямой А 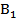 и плоскостью ВД
и плоскостью ВД 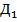 .
.

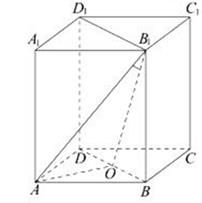


17. Решите неравенство: 3 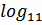 (
(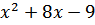 ) ≤ 4+
) ≤ 4+ 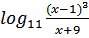 .
.

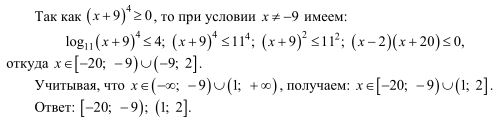
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного включением/исключением точекx=-9, x=1, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
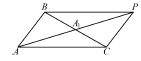
18. Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второй раз пересекает первую окружность в точке А, а вторую в точке D. Прямая, проходящая через точку Q параллельно AD, второй раз пересекает первую окружность в точке В, а вторую – в точке С.
а) Докажите, что четырёхугольник ABCD – параллелограмм.
б) Найдите отношение BP: PC, если радиус первой окружности вдвое больше радиуса второй.
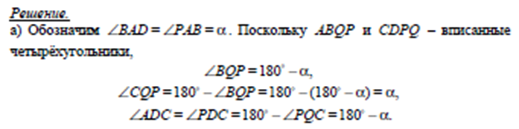

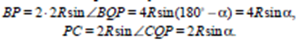
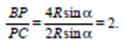
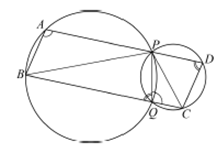
Ответ 2.
| Содержание критерия | Баллы |
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б | |
| Обоснованно получен верный ответ в пункте б, ИЛИ имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за вычислительной ошибки | |
| Имеется верное доказательство утверждения пункта а, ИЛИ при обоснованном решении пункта б получен неверный ответ из-за вычислительной ошибки, ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
19. Банк под определенный процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счета. Но банк увеличил процент годовыхна 40%. К концу следующего года накоплена сумма в 1,44раза превысила первоначальный вклад. Каков процент новых годовых?
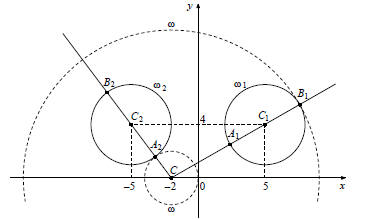
Решение.
От суммы вклада ситуация не изменится. Положим в банк 4 рубля (делится на 4), равной (4p) рублей.
Поделим её на 4 части, унесём домой (p) рублей, оставим в банке (3p) рублей.
Известно, что к концу следующего года в банке оказалось
4·1,44 = 5,76 рублей.
Итак, число (3p) превратилось в число (5,76). Во сколько раз оно увеличилось?
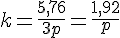
Таким образом, найден второй повышающий коэффициент k банка.
Произведение обоих коэффициентов равно 1,92:
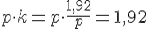
Из условия следует, что второй коэффициент на 0,4 больше первого.
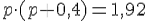
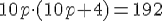
сделаем замену t = 10р:
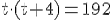
Итак, p = 1,2, k = 1,6.
В 1,2 раза увеличилась сумма вклада первый раз, в 1,6 раз - во второй раз.
Было 100%, стало 160%. Новый процент годовых равен 160%-100% = 60%.
Ответ: 60%
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| Верно построена математическая модель, решение сведено к исследованию этой модели, получен неверный ответ из-за вычислительной ошибки ИЛИ верно построена и исследована математическая модель, получен верный ответ, но решение недостаточно обосновано | |
| Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
20. Найдите все положительные значения а, при каждом из которых сиcтема
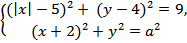 имеет единственное решение.
имеет единственное решение.
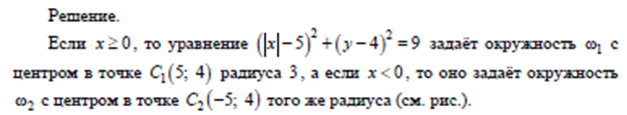



21. Набор состоит из 39 натуральных чисел, среди которых есть числа 4, 5 и 7. Среднее арифметическое любых 34 чисел этого набора меньше 2.
а) Может ли такой набор содержать ровно 16 единиц?
б) Может ли такой набор содержать менее 16 единиц?
в) Докажите, что в любом таком наборе есть несколько чисел, сумма которых равна 35.



| Содержание критерия | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получен один из следующих результатов: – обоснованное решение в п. а, – пример в п. б, – искомая оценка в п. в, – пример в п. в, обеспечивающий точность предыдущей оценки | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
вариант 2
15.а) Решите уравнение: 6· 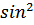 x+5
x+5  (
( –x)– 2 =
–x)– 2 = 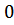
б) Найдите все корни этого уравнения, принадлежащие промежутку [-5П; - 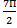 ].
].


| Содержание критерия | Баллы |
| Обоснованно получены верные ответы в обоих пунктах | |
| Обоснованно получен верный ответ в пункте а или в пункте б, ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов – пункта а и пункта б | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
16. В правильной шестиугольной призме ABCDEF 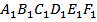 , все рёбра которой
, все рёбра которой
равны 3, найдите расстояние от точки С до прямой 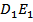 .
.

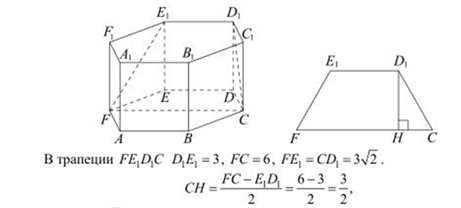 тогда
тогда 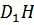 =
= 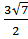 .
.
Ответ: 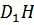 =
= 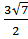 .
.

17. Решите неравенство: 7 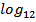 (
(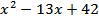 ) ≤ 8+
) ≤ 8+ 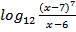 .
.

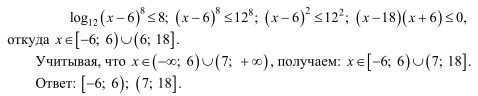
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного включением/исключением точек x=6, x=7, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
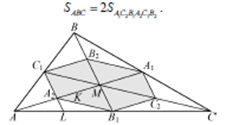
18. Медиана А 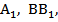 С
С 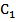 треугольника АВС пересекаются в точке М. Точки
треугольника АВС пересекаются в точке М. Точки 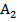 ,
, 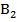 ,
, 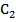 – середины отрезков МА, МВ и МС соответственно.
– середины отрезков МА, МВ и МС соответственно.
а) Докажите, что площадь шестиугольника 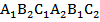 вдвое меньше площади треугольника АВС.
вдвое меньше площади треугольника АВС.
б) Найдите сумму квадратов всех сторон шестиугольника, если известно, что АВ = 5,
ВС = 8, АС = 10.

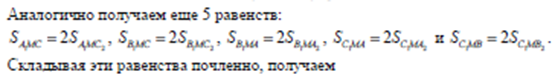

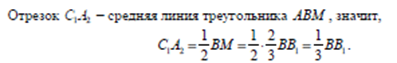
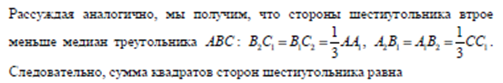
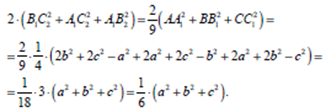 Подставляя в эту формулу длины сторон треугольника АВС, получаем ответ: сумма квадратов сторон шестиугольника равна
Подставляя в эту формулу длины сторон треугольника АВС, получаем ответ: сумма квадратов сторон шестиугольника равна 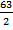
Ответ: 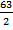
| Содержание критерия | Баллы |
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б | |
| Обоснованно получен верный ответ в пункте б, ИЛИ имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за вычислительной ошибки | |
| Имеется верное доказательство утверждения пункта а, ИЛИ при обоснованном решении пункта б получен неверный ответ из-за вычислительной ошибки, ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
19. Брокерская фирма приобрела два пакета акций, а затем продала их за общую сумму 7 миллионов 680 тысяч рублей, получив при этом 28% прибыли. За какую сумму фирма приобрела каждый из пакетов акций, если при продаже первого пакета прибыль составила 40%, а при продаже второго – 20%?
Решение:
Пусть фирма приобрела первый пакет акций за x рублей, а второй – за y рублей.
при продаже первого пакета прибыль составила 40%, то есть акции были проданы за 1,4x руб.
при продаже второго – 20%, то есть акции были проданы за 1,2y руб.
Фирма продала их за общую сумму 7 миллионов 680 тысяч рублей, то есть
1,4х+1,2у = 7680000 руб.
получив при этом 28% прибыли, следовательно 1,28(х+у)=7680000 руб.Получили систему уравнений:
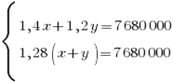 Вычтем из первого уравнения второе. Получим:
Вычтем из первого уравнения второе. Получим:
0,12х – 0,08у = 0, отсюда 12х=8у, или у = 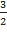 х.
х.
Подставим выражение для у в первое уравнение системы. Получим:
1,4х+1,2 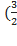 х) = 7680000
х) = 7680000
3,2х=7680000
х=2400000
у=3600000
 2015-04-30
2015-04-30 1465
1465