Прямая задача:
F = 4x1 + 3x2 + x3 + 0*x4 + x5 + 2x6 ® min
 2x2 + 2x3 + 4x4 + x5 ≥ 150
x1+ x2 +2x5 ≥ 200
x1 +x3 2x6 ≥ 300
xj ≥ 0, 2x2 + 2x3 + 4x4 + x5 ≥ 150
x1+ x2 +2x5 ≥ 200
x1 +x3 2x6 ≥ 300
xj ≥ 0, 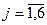
|
Двойственная задача:
L = 150y1 + 200y2 + 300y3 ® max
0*y1 + y2 + y3 ≤ 4
2y1 + y2 + 0*y3 ≤ 3
2y1 + 0*y2 + y3 ≤ 1
4y1 + 0*y2 + 0*y3 ≤ 0
y1 + 2y2 + 0*y3 ≤ 1
0*y1 + 0*y2 + 2y3 ≤ 2
yi ≥ 0, 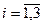
|
В данном случае прямой является задача на минимум. Поэтому двойственная задача строится на максимум (раздел 3.5.1, примечание 1).
Наряду с задачей минимизации потерь бумаги на 1 метр длины стандартного рулона, при использовании шести технологических способов (целевая функция прямой задачи), фирма может решать задачу максимальной экономии бумаги при эффективном использовании технологий раскроя (целевая функция двойственной задачи).
Таким образом, переменные yi (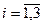 ) являются оценками i -го типа нестандартного рулона, например, могут характеризовать удельную экономию бумаги на 1 метр одного нестандартного рулона соответствующей длины.
) являются оценками i -го типа нестандартного рулона, например, могут характеризовать удельную экономию бумаги на 1 метр одного нестандартного рулона соответствующей длины.
Исходя из данного определения двойственных переменных, ограничения двойственной задачи характеризуют эффективность применения технологических способов раскроя бумаги: в левой части находится суммарная экономия на рулонах трех типов по каждому способу раскроя, а справа – потери на 1 метр длины стандартного рулона как мера эффективности данной технологии.
Естественное условие yi ≥ 0 (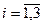 ).
).
Пример 3.9 Задача о рационе (пример 2.3)
Двойственная задача:
L = 60y1 + 50y2 ® max
y1 + 2y2 ≤ 19
3y1 + 4y2 ≤ 24
4y1 + 2y2 ≤ 25
yi ≥ 0, 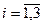
|
Прямая задача:
F = 19x1 + 24x2 + 25x3 ® min
x1 + 3x2 + 4x3 ≥ 60
2x1 + 4x2 + 2x3 ≥ 50
xj ≥0, 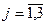
|
Двойственные переменные y1 и y2 выражают оценку питательного вещества A и В соответственно. Таким образом, целевая функция двойственной задачи характеризует суммарную оценку питательных веществ в кормовой смеси, а ограничения отражают рентабельность использования i -го вида корма: в левой части стоит внутренняя суммарная оценка питательных веществ А и В в 1 кг. корма каждого вида, а в правой – внешняя оценка 1 кг. корма i -го вида (цена за 1 кг.).
Итак, рассмотрев четыре пары двойственных задач, можно сделать вывод, что переменные двойственной задачи yi (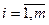 ) в общем случае представляют собой ценность (оценку) i -го ограничения прямой задачи (иногда их называют теневыми ценами). Поэтому, придавая двойственным переменным конкретное экономическое содержание, необходимо исходить из постановки каждой конкретной задачи.
) в общем случае представляют собой ценность (оценку) i -го ограничения прямой задачи (иногда их называют теневыми ценами). Поэтому, придавая двойственным переменным конкретное экономическое содержание, необходимо исходить из постановки каждой конкретной задачи.
 2015-04-30
2015-04-30 985
985








