Пример 4.1 Составить такой план перевозок гравия, при котором потребности в нем каждой из строящихся дорог были бы удовлетворены при наименьшей общей стоимости перевозок

Для строительства четырех дорог используется гравий из трех карьеров. Запасы гравия в каждом из карьеров соответственно равны 120, 280 и 160 тонн потребности в гравии для строительства каждой из дорог соответственно равны 130, 220, 60 и 70 тонн известны также тарифы перевозок 1 тонны гравия из каждого карьера к каждой из строящихся дорог, которые задаются матрицей:

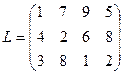
Составить такой план перевозок гравия, при котором потребности в нем каждой из строящихся дорог были бы удовлетворены при наименьшей общей стоимости перевозок.

Построим математическую модель данной задачи. Пусть x_ij – количество тонн гравия, перевозимое из i -го карьера на строительство j -й дороги,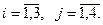

Целевая функция задачи выражает минимальные издержки по транспортировке гравия на строительство трех дорог и имеет вид:

F=1x₁₁+7x₁₂+9x₁₃+5x₁₄+4x₂₁+2x₂₂+6x₂₃+8x₂₄+3x₃₁+8x₃₂+1x₃₃+2x₃₄→min

Балансные ограничения на:

- вывоз гравия из карьеров:

1-го: x₁₁+ x₁₂+ x₁₃+x₁₄ = 120;

2-го: x₂₁+ x₂₂+ x₂₃+ x₂₄ = 280;

3-го: x₃₁+ x₃₂+ x₃₃+ x₃₄ = 160;

- удовлетворение потребности в гравии на строительстве дорог:

1-й: x₁₁+ x₂₁+ x₃₁ = 130;

2-й: x₁₂+ x₂₂+ x₃₂ = 220;

3-й: x₁₃+ x₂₃+ x₃₃ = 60;

4-й: x₁₄+ x₂₄+ x₃₄ = 70;

Естественное ограничение: x_ij ≥ 0,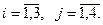

Решение

Исходные данные задачи сведем в таблицу (табл. 4.1).

Таблица 4.1

Пункты отправления Пункты назначения Запасы

В₁ В₂ В₃ В₄

А₁ А₂ А₃

Потребности

Как видно из таблицы 4.1, запасы гравия в карьерах (120+280+160=560) больше, чем потребности в нем (130+220+60+70=480) на строящихся дорогах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительный пункт назначения В₅ с потребностями, равными 560-480=80 тонн. Тарифы перевозки 1 тонны гравия из всех карьеров в пункт В₅ полагаем равным нулю. В результате получаем закрытую модель транспортной задачи (см. таблицу 4.2).

Шаг 1 Найдем начальное допустимое решение методом минимального элемента (метод наименьшей стоимости).

Данный метод заключается в следующем. На каждой итерации заполняется одна из допустимых ячеек транспортной таблицы, пока не будет заполнено n+m-1 ячейка. Выбор ячейки A_iB_j осуществляется по наименьшему тарифу. Каждая выбранная для заполнения ячейка характеризуется двумя числами a_i и b_j, записанными в строке и столбце, на пересечении которых стоит данная ячейка. Из этих чисел выбирается 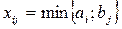. При этом исчерпывается либо строка (a_i' = 0), либо столбец (b_j' = 0), либо одновременно и строка, и столбец (a_i' = b_j' = 0). Таким образом, после заполнения ячейки A_iB_j необходимо пересчитать остатки в данных строке и столбце по следующему правилу:

a_i' = 0, b_j' = b_j - a_i, если a_i < b_j, (а)

b_j' = 0, a_i' = a_i - b_j, если a_i > b_j, (в)

a_i'= b_j' = 0, если a_i = b_j. (с)

Затем выбирают новую допустимую ячейку для заполнения по наименьшему из оставшихся тарифов. Причем в случае (а) исчерпывается i -я строка, а в случае (в) – j -й столбец таблицы. Ячейки из этой строки (столбца) становятся недопустимыми для заполнения и из дальнейшего рассмотрения исключаются. Заполнение таблицы прекращается после того, как записаны в ячейки n+m-1 положительные переменные.