1. Замена переменных в неопределенном интеграле
Если
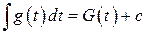 ,
,
то тогда
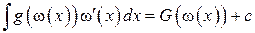 . (4.1)
. (4.1)
Пусть требуется вычислить интеграл
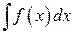
Выбирая в качестве новой переменной функцию 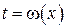 , такую что подынтегральное выражение представляется в виде
, такую что подынтегральное выражение представляется в виде
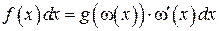
Цель данного приема состоит к переходу более удобной для интегрирования функции 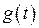 .
.
Пример. 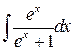 . Вводя
. Вводя 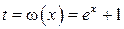 , получаем
, получаем
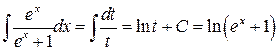
2. Интегрирование по частям
Этот прием представляет сведение данного интеграла 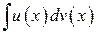 к интегралу
к интегралу 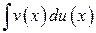 с помощью формулы
с помощью формулы
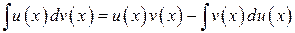 (4.2)
(4.2)
Этот прием ведет к цели, если 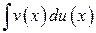 находится легче, чем
находится легче, чем 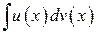 .
.
Это правило хотя и имеет более ограниченную область применения по сравнению с заменой переменной, существует целый класс функций, который интегрируется именно с помощью этого метода. Сюда можно отнести:
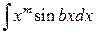
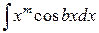
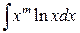
где 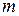 есть любое целое положительное число.
есть любое целое положительное число.
Применение формулы (4.2) предусматривает последовательное понижение степени 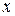 до нулевой.
до нулевой.
3. Интегрирование простых дробей
К простым дробям относятся
1) 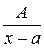 ; 2)
; 2) 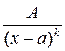 ; 3)
; 3) 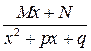 ; 4)
; 4) 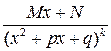
где 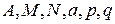 - действительные числа,
- действительные числа, 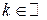 . Кроме того, трехчлен
. Кроме того, трехчлен 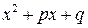 не имеет действительных корней, т.е.
не имеет действительных корней, т.е.
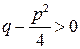
Интегрирование (1) и (2) не представляет трудностей:
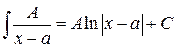 (4.3)
(4.3)
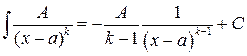 (4.4)
(4.4)
Для интегрирования дроби (3) применим метод замены переменной. Выделяя сначала из знаменателя полный квадрат
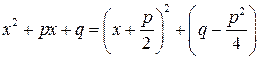
и прибегнув к подстановке
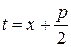
и обозначив
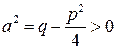
получаем
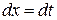
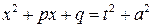
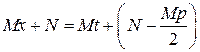
а сам интеграл
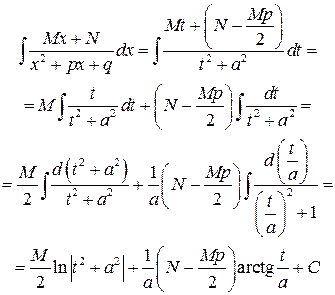
Возвращаясь обратно к переменной 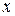 окончательно получаем:
окончательно получаем:
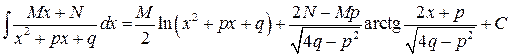 (4.5)
(4.5)
Для случая (4) подстановка 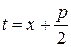 приводит
приводит
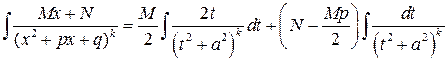
Первый интеграл вычисляется подстановкой 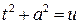 ,
, 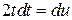 :
:
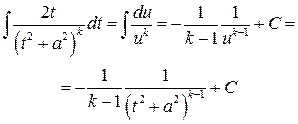 (4.6)
(4.6)
Второй интеграл вычисляется с помощью рекуррентной формулы
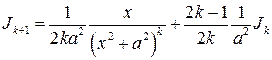 (4.7)
(4.7)
где
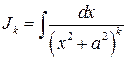
Формула (4.7) позволяет вычислить искомый интеграл для любого натурального индекса 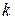 .
.
Так как при 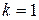
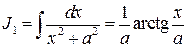
то по формуле (4.7) найдем
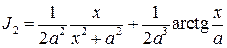 и т.д.
и т.д.
4. Интегрирование дробно-рациональных функций
Дробно-рациональной функцией (дробью) называется выражение вида
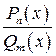
где 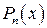 и
и 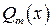 — многочлены степени
— многочлены степени 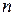 и
и 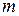 , не имеющие общих корней, т.е.
, не имеющие общих корней, т.е.
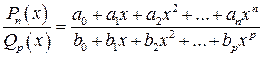 (4.8)
(4.8)
Дробь (4.8) называется правильной если 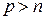 ; неправильной в противном случае. Каждую неправильную дробь можно привести к правильной путем исключения целой части, интегрирование которой не представляет сложностей.
; неправильной в противном случае. Каждую неправильную дробь можно привести к правильной путем исключения целой части, интегрирование которой не представляет сложностей.
В курсе высшей алгебры доказывается важная теорема, о том, что любая правильная дробь (4.8) может быть представлена в виде конечного числа правильных дробей.
Если 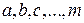 — корни уравнения
— корни уравнения 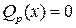 , а
, а 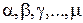 — их соответствующие кратности, так что
— их соответствующие кратности, так что
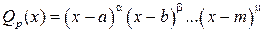
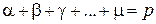
то дробь (4.8) представляется в виде
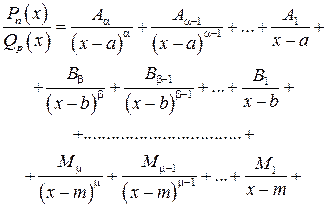 (4.9)
(4.9)
где числители отдельных дробей определяются из системы линейных уравнений после приведения к общему знаменателю и приравнивания коэффициентов при одинаковых степенях с 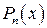 (метод неопределенных коэффициентов).
(метод неопределенных коэффициентов).
Если 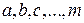 — простые корни уравнения
— простые корни уравнения 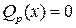 , т.е.
, т.е. 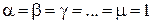 , то
, то
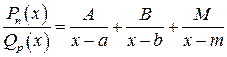
Если некоторые корни уравнения 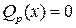 мнимы, то, соединяя вместе элементарные дроби, соответствующие сопряженным корням, можно после некоторых преобразований соответствующие пары дробей представить в виде действительных дробей вида
мнимы, то, соединяя вместе элементарные дроби, соответствующие сопряженным корням, можно после некоторых преобразований соответствующие пары дробей представить в виде действительных дробей вида
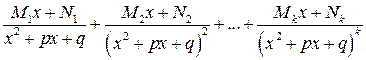 .
.
и методом неопределенных коэффициентов найти неизвестные 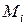 и
и 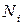
Таким образом, интегрирование правильной рациональной дроби 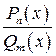 приводится к интегралам вида
приводится к интегралам вида
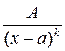
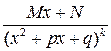
рассмотренных в предыдущем п.3.
5. Интегрирование некоторых выражений, содержащих радикалы
Интегралы вида
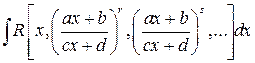 (4.10)
(4.10)
где 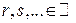 — рациональные числа, приводятся к интегралам от рациональных функций подстановкой
— рациональные числа, приводятся к интегралам от рациональных функций подстановкой
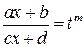 (4.11)
(4.11)
где 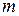 общий знаменатель дробей
общий знаменатель дробей 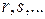 .
.
Интегралы вида
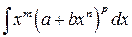 (4.12)
(4.12)
(интегралы от биномиальных дифференциалов), где 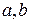 — действительные числа, а
— действительные числа, а 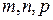 — рациональные, выражаются в элементарных функциях только в следующих случаях:
— рациональные, выражаются в элементарных функциях только в следующих случаях:
а) когда 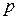 — целое число; тогда этот интеграл имеет вид суммы интегралов (4.10);
— целое число; тогда этот интеграл имеет вид суммы интегралов (4.10);
б) когда 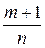 — целое число; подстановкой; подстановкой
— целое число; подстановкой; подстановкой 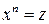 этот интеграл преобразуется к виду (4.10)
этот интеграл преобразуется к виду (4.10)
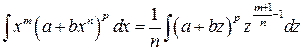 (4.13)
(4.13)
в) когда 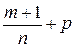 — целое число; при помощи той же подстановки
— целое число; при помощи той же подстановки 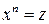 данный интеграл приводится к виду (4.10)
данный интеграл приводится к виду (4.10)
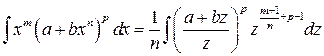 (4.14)
(4.14)
Рационализация подынтегрального выражения в интегралах вида
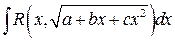
достигается с помощью, по крайней мере, одной из следующих трех подстановок, называемых подстановками Эйлера
а) 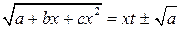 при
при 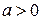 ;
;
б) 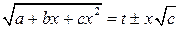 при
при 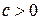 ;
;
в) 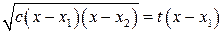 при условии, что корни
при условии, что корни 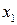 и
и 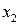 уравнения
уравнения 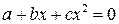 действительны.
действительны.
6. Интегрирование тригонометрических выражений
Интегралы вида
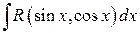 (4.14)
(4.14)
могут быть всегда приведены к интегралам от рациональных функций при помощи подстановки
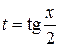 (4.15)
(4.15)
При этом функции подынтегрального выражения выражаются через новые переменные
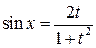 ;
; 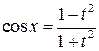 ;
; 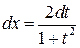 (4.16)
(4.16)
Если при этом подынтегральная функция 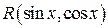 удовлетворяет соотношению
удовлетворяет соотношению
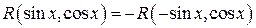 (4.17)
(4.17)
то выгодно применить подстановку 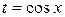 . Например, с помощью этой подстановки интеграл
. Например, с помощью этой подстановки интеграл
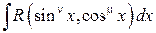 (4.18)
(4.18)
где 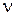 — нечетное число, а
— нечетное число, а 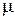 — четное, с соответствующей заменой
— четное, с соответствующей заменой
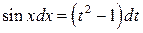 (4.19)
(4.19)
приводится к интегралу от рациональной функции.
Если эта функция удовлетворяет соотношению
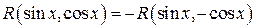 (4.20)
(4.20)
то выгодно применить подстановку 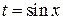 . Например, с помощью этой подстановки интеграл
. Например, с помощью этой подстановки интеграл
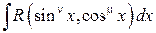 (4.21)
(4.21)
где 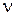 — четное число, а
— четное число, а 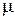 — нечетное, с соответствующей заменой
— нечетное, с соответствующей заменой
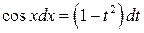 (4.22)
(4.22)
приводится к интегралу от рациональной функции.
Если эта функция удовлетворяет соотношению
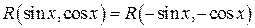 (4.23)
(4.23)
то выгодно применить подстановку 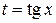 . Например, с помощью этой подстановки интеграл
. Например, с помощью этой подстановки интеграл
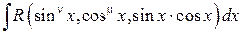 (4.24)
(4.24)
где 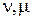 — четные числа, с соответствующей заменой
— четные числа, с соответствующей заменой
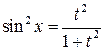 ;
; 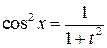 ;
; 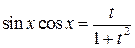
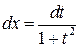 (4.25)
(4.25)
приводится к интегралу от рациональной функции.
7. Интегрирование выражений, содержащих гиперболические функции
Интегралы вида
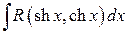 (4.26)
(4.26)
могут быть всегда приведены к интегралам от рациональных функций при помощи подстановки
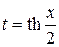 (4.27)
(4.27)
При этом функции подынтегрального выражения выражаются через новые переменные
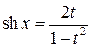 ;
; 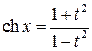 ;
; 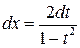 (4.22)
(4.22)
 2015-04-30
2015-04-30 2909
2909
