1. Интегралы вида 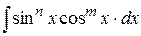 , где m и n – натуральные числа.
, где m и n – натуральные числа.
(a) Среди показателей степеней n и m есть хотя бы одно нечетное число. В этом случае используем прием подведения множителя под знак дифференциала.
Пример 7.11. 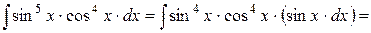
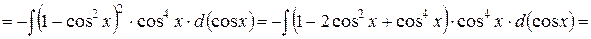
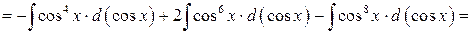
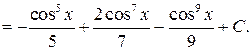
(b) Оба показателя степени n и m – четные числа. В этом случае применяем тригонометрические формулы понижения степени:
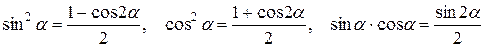 .
.
Пример 7.12. 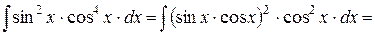
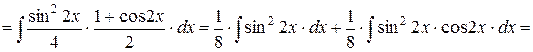
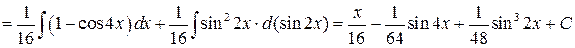 .
.
2. Интегралы вида
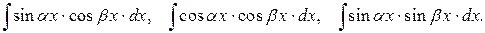
В данном случае, применяя известные тригонометрические тождества
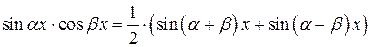 ,
,
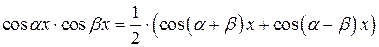 ,
, 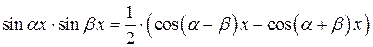 ,
,
можно интеграл от произведения двух тригонометрических функций свести к интегрированию суммы двух тригонометрических функций.
Пример 7.13. 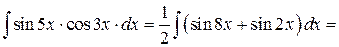
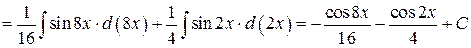 .
.
3. Универсальная тригонометрическая подстановка.
Интегралы вида 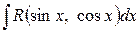 , где
, где 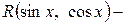 рациональная функция от sin x и cos x, можно свести к интегралам от частного двух многочленов. Это можно сделать при помощи так называемой универсальной тригонометрической подстановки:
рациональная функция от sin x и cos x, можно свести к интегралам от частного двух многочленов. Это можно сделать при помощи так называемой универсальной тригонометрической подстановки: 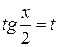 . При этом
. При этом
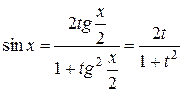 ,
, 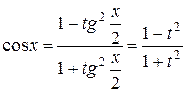 ,
,
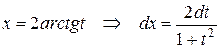 .
.
Пример 7.14. 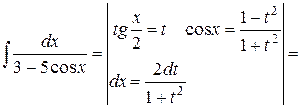
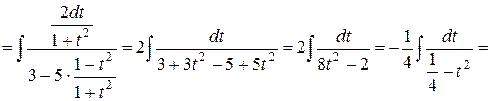
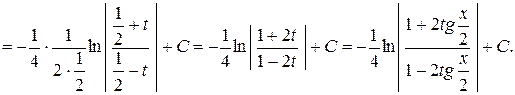
Мы воспользовались табличной формулой 11.
Глава 8. Определенный интеграл.
Несобственные интегралы
§8.1. Задача о площади криволинейной трапеции.
Определение определенного интеграла
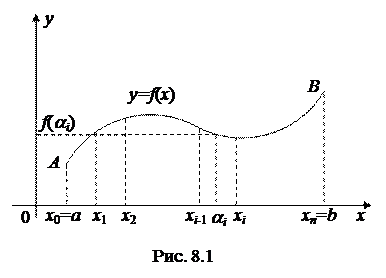 Предположим, нам требуется найти площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f (x), где f (x) – некоторая непрерывная неотрицательная на отрезке [ a; b ] функция (рис. 8.1).
Предположим, нам требуется найти площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f (x), где f (x) – некоторая непрерывная неотрицательная на отрезке [ a; b ] функция (рис. 8.1).
Разобьем отрезок [ a; b ] точками 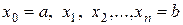 на n частей. Выберем на каждом из полученных отрезков произвольную точку
на n частей. Выберем на каждом из полученных отрезков произвольную точку 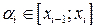 . При этом криволинейная трапеция вертикальными прямыми
. При этом криволинейная трапеция вертикальными прямыми 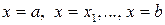 разбивается на n полос, каждую из которых условно можно считать прямоугольником. Длина основания i -го прямоугольника равна D xi = xi – xi – 1, а за высоту приближенно можно принять значение функции y = f (x) в точке ai
разбивается на n полос, каждую из которых условно можно считать прямоугольником. Длина основания i -го прямоугольника равна D xi = xi – xi – 1, а за высоту приближенно можно принять значение функции y = f (x) в точке ai 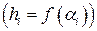 . Таким образом, площадь i -й полосы приближенно равна
. Таким образом, площадь i -й полосы приближенно равна 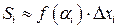 . Площадь всей криволинейной трапеции складывается из площадей составляющих ее полос:
. Площадь всей криволинейной трапеции складывается из площадей составляющих ее полос:
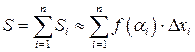 . (8.1)
. (8.1)
Равенство (8.1) тем точнее выражает площадь криволинейной трапеции, чем каждая из составляющих ее полос больше напоминает прямоугольник, то есть, чем меньше каждое D xi.
Дадим теперь определение определенного интеграла. Пусть f (x) – произвольная функция, определенная на отрезке [ a; b ] (см. рис. 8.1). Разобьем отрезок [ a; b ] точками 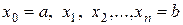 на n частей и выберем на каждом из полученных отрезков произвольную точку
на n частей и выберем на каждом из полученных отрезков произвольную точку 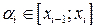 . В полученных точках вычислим значения функции
. В полученных точках вычислим значения функции 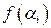 и вычислим сумму
и вычислим сумму 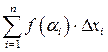 (данная сумма называется интегральной).
(данная сумма называется интегральной).
2 Предел интегральной суммы при 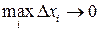 , если он существует, конечен и не зависит от способа разбиения отрезка [ a; b ] на части, и от выбора точек
, если он существует, конечен и не зависит от способа разбиения отрезка [ a; b ] на части, и от выбора точек 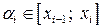 , называется определенным интегралом от функции f (x) на промежутке [ a; b ] и обозначается
, называется определенным интегралом от функции f (x) на промежутке [ a; b ] и обозначается 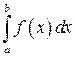 . Таким образом,
. Таким образом,
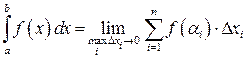 . (8.2)
. (8.2)
Замечание. Условие 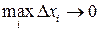 означает, что длина каждого из отрезков
означает, что длина каждого из отрезков 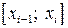 стремится к нулю, а это возможно лишь тогда, когда число разбиений стремится к бесконечности (n ® ¥). Обратное утверждение не верно. При n ® ¥ могут остаться отрезки
стремится к нулю, а это возможно лишь тогда, когда число разбиений стремится к бесконечности (n ® ¥). Обратное утверждение не верно. При n ® ¥ могут остаться отрезки 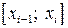 , длины которых не стремятся к нулю. Таким образом, в определении определенного интеграла условие
, длины которых не стремятся к нулю. Таким образом, в определении определенного интеграла условие 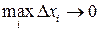 нельзя заменить условием n ® ¥.
нельзя заменить условием n ® ¥.
1 Для любой непрерывной на промежутке [ a; b ] функции f (x) существует определенный интеграл 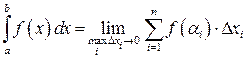 .
.
1 Площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f (x), где f (x) – некоторая непрерывная неотрицательная функция равна:
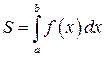 . (8.3)
. (8.3)
В этом заключается геометрический смысл определенного интеграла.
§8.2. Свойства определенного интеграла.
Формула Ньютона-Лейбница
Перечислим без доказательства основные свойства определенного интеграла от непрерывной на отрезке [ a; b ] функции f (x).
1. Постоянный множитель можно выносить за знак определенного интеграла:
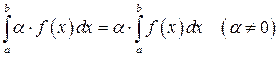 . (8.4)
. (8.4)
2. Определенный интеграл от суммы двух (или нескольких) функций равен сумме интегралов от этих функций:
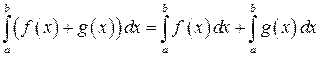 . (8.5)
. (8.5)
3. Пусть с – произвольная точка из промежутка [ a; b ], тогда:
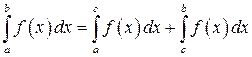 . (8.6)
. (8.6)
4. При изменении порядка интегрирования, определенный интеграл меняет знак на противоположный:
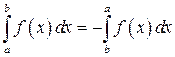 . (8.7)
. (8.7)
5. Теорема о среднем значении. Внутри интервала (a; b) существует такая точка с, что
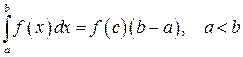 . (8.8)
. (8.8)
6. Оценка определенного интеграла
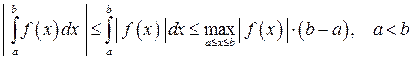 . (8.9)
. (8.9)
При доказательстве этих и других свойств используется определение определенного интеграла (формула (8.2)), однако, при решении практических задач пользоваться определением определенного интеграла крайне затруднительно. Обычно в таких случаях применяется формула Ньютона-Лейбница в сочетании со свойствами определенного интеграла, или приближенные методы.
1 Если функция интегрируема на промежутке [ a, b ], то она на
[ a, b ] имеет непрерывную первообразную. Это, в частности, справедливо когда f (x) непрерывна.
1 Формула Ньютона-Лейбница:
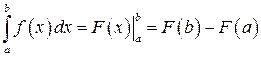 . (8.10)
. (8.10)
Здесь через F (x) обозначена первообразная функции f (x) на промежутке [ a; b ].
Задача 8.1. Вычислить определенный интеграл: 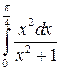 .
.
Решение. 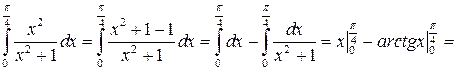
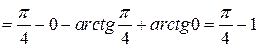 .
.
При вычислении данного интеграла, мы воспользовались 1-м и 2-м свойствами определенного интеграла и формулой Ньютона-Лейбница.
Задача 8.2. Вычислить определенный интеграл: 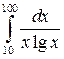 .
.
Решение. Умножим и разделим подынтегральную функцию на ln10 и внесем множитель 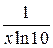 под знак дифференциала:
под знак дифференциала:
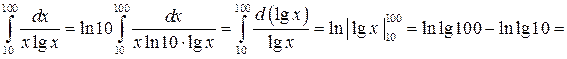
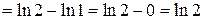 .
.
§8.3. Замена переменной и интегрирование по частям
под знаком определенного интеграла
Замену переменной под знаком определенного интеграла в отличие от замены переменной под знаком неопределенного интеграла осуществляют, учитывая два обстоятельства:
1. В ходе замены переменной необходимо изменить пределы интегрирования. Так, если старыми пределами интегрирования являлись числа x 1 и x 2, и мы осуществили подстановку 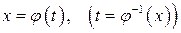 , то новыми пределами интегрирования будут числа
, то новыми пределами интегрирования будут числа 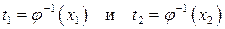 .
.
2. После нахождения первообразной 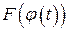 нет необходимости возвращаться к старой переменной x, нужно лишь в соответствие с формулой Ньютона-Лейбница подставить в нее новые пределы интегрирования t 1 и t 2:
нет необходимости возвращаться к старой переменной x, нужно лишь в соответствие с формулой Ньютона-Лейбница подставить в нее новые пределы интегрирования t 1 и t 2:
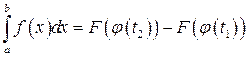 .
.
Задача 8.3. Вычислить определенный интеграл: 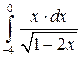 .
.
Решение. 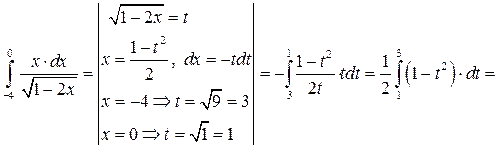
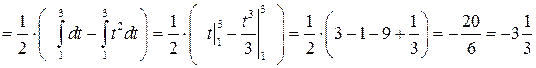 .
.
1 Формула интегрирования по частям в случае определенного интеграла имеет вид:
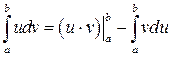 . (8.11)
. (8.11)
Задача 8.4. Вычислить интеграл: 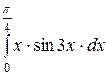 .
.
Решение. 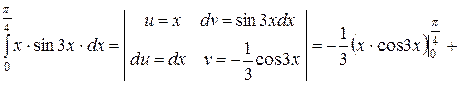
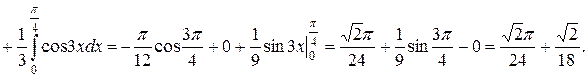
§8.4. Приложения определенных интегралов
1. Вычисление площадей плоских фигур
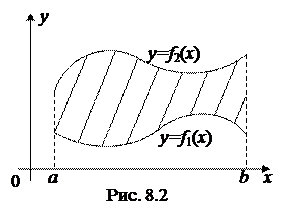 g Площадь фигуры, ограниченной линиями x = a, x = b, y = f 1(x), y = f 2(x), где f 1(x) и f 2(x) – некоторые непрерывные на отрезке [ a; b ] функции, причем
g Площадь фигуры, ограниченной линиями x = a, x = b, y = f 1(x), y = f 2(x), где f 1(x) и f 2(x) – некоторые непрерывные на отрезке [ a; b ] функции, причем 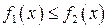 (рис. 8.2), можно найти по формуле
(рис. 8.2), можно найти по формуле
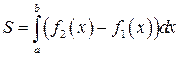 . (8.12)
. (8.12)
4 Без ограничения общности, можно считать, что 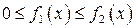 . В противном случае обе функции можно увеличить на одну и ту же константу (при этом графики обеих функций сместятся вверх) такую, что новые функции окажутся неотрицательными.
. В противном случае обе функции можно увеличить на одну и ту же константу (при этом графики обеих функций сместятся вверх) такую, что новые функции окажутся неотрицательными.
Из рисунка 8.2 видно, что искомая площадь равна разности площадей двух криволинейных трапеций 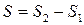 . Каждую из площадей S 1 и S 2 можно найти по формуле (8.3). Следовательно
. Каждую из площадей S 1 и S 2 можно найти по формуле (8.3). Следовательно
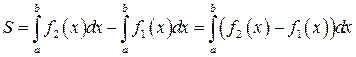 . 3
. 3
Задача 8.5. Вычислить площадь земельного участка, ограниченного линиями 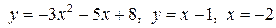 .
.
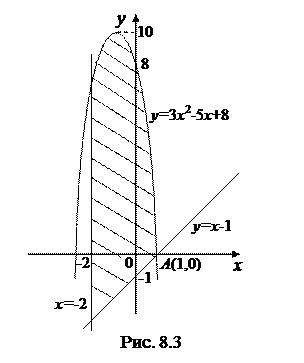
Решение. Построим данные линии в декартовой системе координат (рис. 8.3). Земельный участок изображен заштрихованным. Найдем точку А пересечения параболы с прямой y = x – 1. Для этого решим систему:
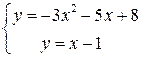 .
.
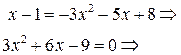
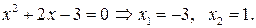
Таким образом, 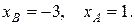
Искомую площадь найдем по формуле (8.12):
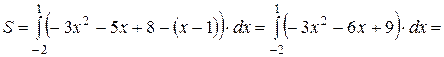
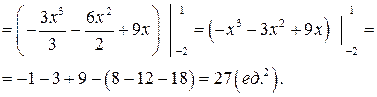
g Пусть криволинейная трапеция (рис. 8.1) сверху ограничена графиком функции, заданной параметрически 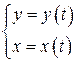 на некотором отрезке [ t 1; t 2], причем функция y (t) является непрерывной, а функция x (t) – непрерывно-дифференцируемой на данном отрезке. Тогда площадь S криволинейной трапеции находится по формуле:
на некотором отрезке [ t 1; t 2], причем функция y (t) является непрерывной, а функция x (t) – непрерывно-дифференцируемой на данном отрезке. Тогда площадь S криволинейной трапеции находится по формуле:
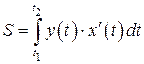 . (8.13)
. (8.13)
4Формула (8.13) получена из формулы (8.3), если в последней произвести замену переменной:
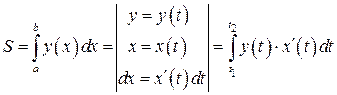 .
.
Новые пределы интегрирования t 1 и t 2 находятся из систем 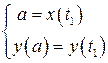 ,
, 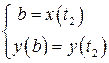 . Они соответствуют началу и концу дуги, соответственно.3
. Они соответствуют началу и концу дуги, соответственно.3
Задача 8.6. Вычислить площадь, ограниченную первой аркой циклоиды
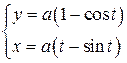 .
.
 Решение. Построим первую арку циклоиды по точкам:
Решение. Построим первую арку циклоиды по точкам:
| t | 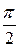 | 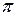 | 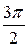 | 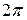 | ||
| x | 0.57 a | 3.14 a | 5.71 a | 6.28 a | ||
| y | a | 2 a | a |
Таким образом, началу арки (точке А) соответствует значение параметра t 1 = 0, вершине (точке В) – значение t 2 = p, и концу (точке С) – значение t 3 = 2 p. Площадь всей арки циклоиды можно найти, вычислив площадь половины арки S 1 (рис. 8.4). По формуле 8.13 получим
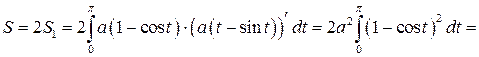
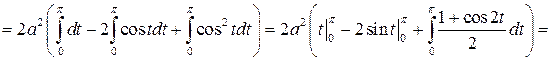
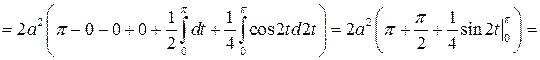
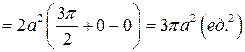 .
.
2. Вычисление длины дуги плоской кривой
1 Предположим, что на плоскости некоторая дуга (кривая линия)  является графиком непрерывно-дифференцируемой функции y = f (x) на отрезке
является графиком непрерывно-дифференцируемой функции y = f (x) на отрезке
[ a; b ] (рис. 8.1). В этом случае длину l дуги 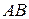 можно вычислить по формуле:
можно вычислить по формуле:
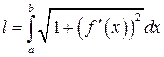 . (8.14)
. (8.14)
1 Предположим, что дуга 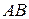 (рис. 8.1) является графиком функции, заданной параметрически
(рис. 8.1) является графиком функции, заданной параметрически 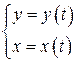 на некотором отрезке [ t 1; t 2], причем функции y (t) и x (t) непрерывно-дифференцируемы на данном отрезке. Тогда длину l дуги
на некотором отрезке [ t 1; t 2], причем функции y (t) и x (t) непрерывно-дифференцируемы на данном отрезке. Тогда длину l дуги 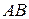 можно вычислить по формуле:
можно вычислить по формуле:
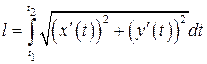 . (8.15)
. (8.15)

Задача 8.7. Вычислить длину дуги полукубической параболы 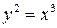 на промежутке [0; 1] (рис. 8.5).
на промежутке [0; 1] (рис. 8.5).
Решение. Полукубическая парабола состоит из двух симметричных относительно оси OX ветвей 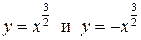 . Искомая длина l равна сумме длин дуг
. Искомая длина l равна сумме длин дуг 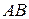 (l 1) и
(l 1) и 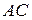 (l 2). Так как длины дуг
(l 2). Так как длины дуг 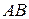 и
и 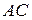 совпадают, то l =2 l 1.
совпадают, то l =2 l 1.
Таким образом, по формуле (8.14) мы получим:
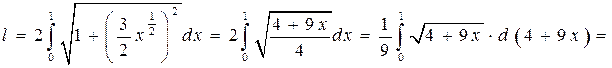
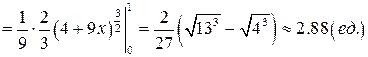 .
.
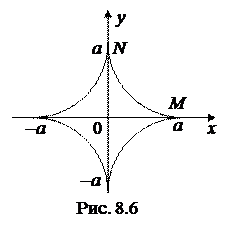
Задача 8.8. Вычислить длину астроиды
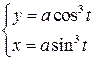 (рис. 8.6).
(рис. 8.6).
Решение. Астроиду, так же как и циклоиду (задача 8.6) можно построить по точкам (в качестве упражнения сделайте это самостоятельно). Астроида состоит из четырех равных по длине частей. Найдем длину дуги астроиды, расположенной в первой четверти, и умножим ее на четыре. Началу дуги (точке N) соответствует значение параметра 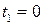 , концу дуги (точке M) соответствует значение параметра
, концу дуги (точке M) соответствует значение параметра 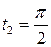 .
.
Таким образом, по формуле (8.15) находим длину астроиды:
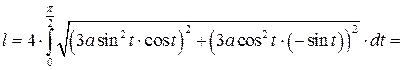
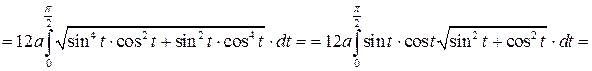
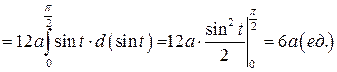 .
.
3. Вычисление объема тела с известным поперечным сечением.
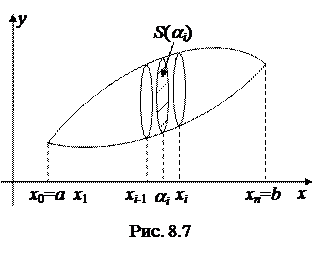 Предположим, что проекцией некоторого тела на ось OX является отрезок [ a; b ] (рис. 8.7). Предположим, что в каждой точке x отрезка [ a; b ] нам известна площадь S (x) поперечного сечения данного тела. Разобьем отрезок [ a; b ] точками
Предположим, что проекцией некоторого тела на ось OX является отрезок [ a; b ] (рис. 8.7). Предположим, что в каждой точке x отрезка [ a; b ] нам известна площадь S (x) поперечного сечения данного тела. Разобьем отрезок [ a; b ] точками 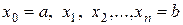 на n частей и проведем в каждой из полученных точек плоскость, перпендикулярную оси OX. При достаточно большом числе разбиений отрезка
на n частей и проведем в каждой из полученных точек плоскость, перпендикулярную оси OX. При достаточно большом числе разбиений отрезка
[ a; b ], тело разрезается на большое количество частей (слоев), каждую из которых приближенно можно считать цилиндром. Высота i -го слоя (цилиндра) равна D xi = xi – xi – 1.
За площадь основания i -го цилиндра примем 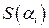 , где
, где 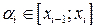 – произвольная точка i -го отрезка. Тогда объем i -го слоя приближенно равен
– произвольная точка i -го отрезка. Тогда объем i -го слоя приближенно равен 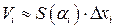 , следовательно, объем тела равен
, следовательно, объем тела равен
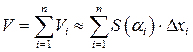 . (8.16)
. (8.16)
Но сумма в формуле (8.16) является интегральной суммой для определенного интеграла 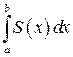 . Таким образом, если функция S (x) является непрерывной на отрезке [ a; b ], то объем тела с известным поперечным сечением S (x) равен
. Таким образом, если функция S (x) является непрерывной на отрезке [ a; b ], то объем тела с известным поперечным сечением S (x) равен
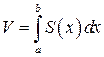 . (8.17)
. (8.17)
4. Вычисление объема тела вращения
 Предположим, что на промежутке
Предположим, что на промежутке
[ a; b ] определена непрерывная функция
y = f (x). Найдем объем тела, которое получается при вращении графика данной функции вокруг оси OX на данном промежутке. Любое сечение данного тела плоскостью, перпендикулярной оси OX, является кругом (рис. 8.8). Радиус круга в произвольной точке x Î[ a; b ] равен значению функции f (x) в этой точке. Следовательно, площадь круга равна 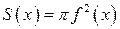 . Подставляя S (x) в формулу (8.17), мы получим формулу объема тела вращения:
. Подставляя S (x) в формулу (8.17), мы получим формулу объема тела вращения:
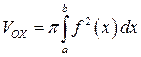 . (8.18)
. (8.18)
 Задача 8.9. Вычислить объем веретена (рис. 8.9), полученного при вращении вокруг оси OX участка синусоиды, расположенного на промежутке [0; p ].
Задача 8.9. Вычислить объем веретена (рис. 8.9), полученного при вращении вокруг оси OX участка синусоиды, расположенного на промежутке [0; p ].
Решение. Искомый объем тела вращения найдем по формуле (8.18):
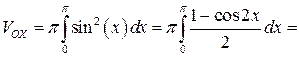
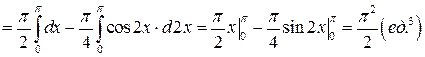
 2015-04-01
2015-04-01 7199
7199
