1. Для вычисления определенного интеграла основной является теорема Ньютона – Лейбница: если 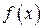 непрерывна на
непрерывна на 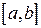 и
и 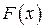 первообразная для
первообразная для 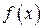 на
на 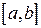 , то
, то
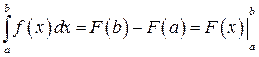 (4.23)
(4.23)
2. Пусть 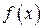 — функция, интегрируемая на
— функция, интегрируемая на 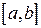 ,
,  ,
, 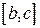 . Тогда, независимо от независимо от взаимного расположения точек
. Тогда, независимо от независимо от взаимного расположения точек 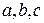 она интегрируема и в двух других промежутках, и имеет место равенство
она интегрируема и в двух других промежутках, и имеет место равенство
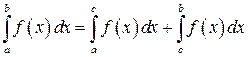 (4.24)
(4.24)
3. Имеют место формулы:
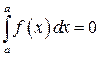 и
и 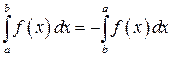 (4.25)
(4.25)
4. Пусть 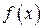 и
и 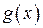 — функции, интегрируемые на
— функции, интегрируемые на 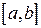 . Тогда, произведение
. Тогда, произведение 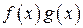 также интегрируемо на этом отрезке.
также интегрируемо на этом отрезке.
5. Если 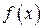 — функция, интегрируемая на
— функция, интегрируемая на 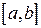 , и
, и 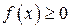 для
для  , то
, то 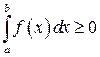 .
.
6. Если 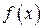 и
и 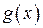 — функции, интегрируемые на
— функции, интегрируемые на 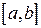 , и
, и 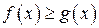 для
для  , то
, то 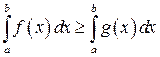 .
.
7. Теорема о среднем значении. Пусть 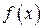 интегрируема и ограничена на
интегрируема и ограничена на 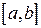 и
и 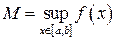 ,
, 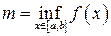 — соответственно, верхняя и нижняя грани
— соответственно, верхняя и нижняя грани 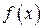 на
на 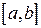 . Тогда, существует такое число
. Тогда, существует такое число 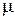 , что:
, что:
1) 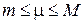 ; и, 2)
; и, 2) 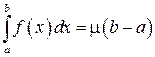 .
.
 2015-04-30
2015-04-30 391
391








