2015-04-30
364
Если каждая из функци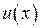й 
и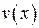 
имеет на отрезке 
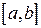непрерывную производную, то справедлива следующая формула
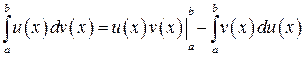
Геометрические приложения определенного интеграла
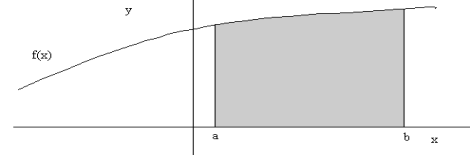
1. Площадь криволинейной трапеции
Площадь фигуры, называемой криволинейной трапецией, лежащей под графиком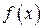 
и неотрицательной на отрезке 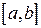равна
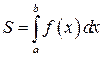
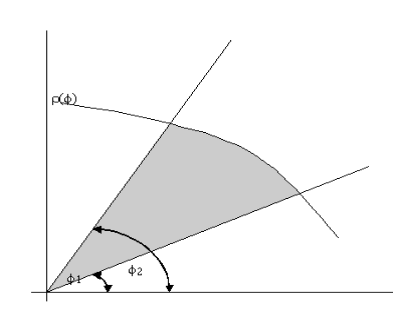
2. Площадь криволинейного сектора
Площадь фигуры, называемой криволинейным сектором, ограниченной графиком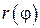 
и двумя лучами, составляющими с полярной осью углы 
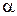и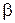 
имеет площадь
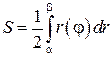
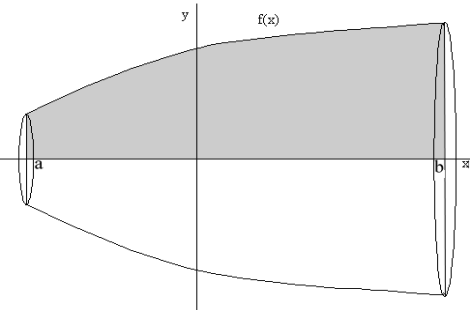
3. Вычисление объема вращения
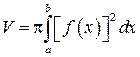
4. Длина дуги кривой.
Если плоская кривая L задана параметрически
, 
,
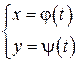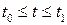причем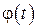 
и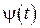 
- непрерывно дифференцируемые функции, то она имеет длину, вычисляемую по следующей формуле
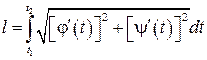
Если плоская кривая L – график непрерывно дифференцируемой функци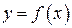и 
и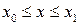 
, то длина этой кривой вычисляется по формуле
В полярных координатах
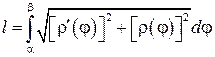
Примеры
Задача 1.Вычислить интеграл:
.
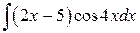Решение: применяя интегрирование по частям, получаем
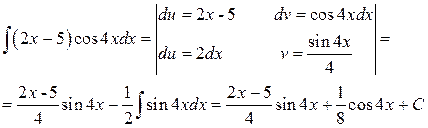
Задача №2:
Вычислить интеграл: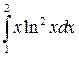 
Решение:
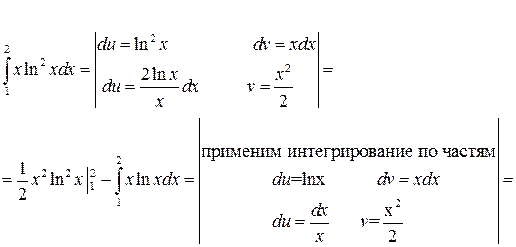
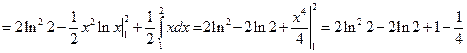
Задача №3:
Вычислить интеграл: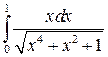 
Решение:
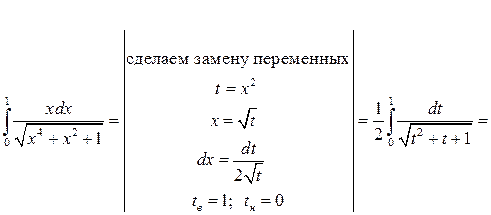
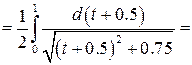
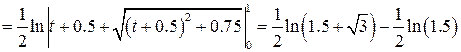
Задача №4:
Вычислить интеграл: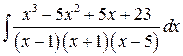 
Решение:
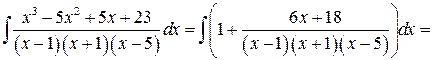
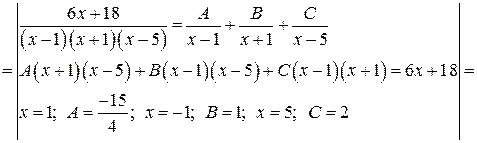
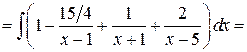
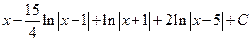
Задача №5:
Вычислить интеграл: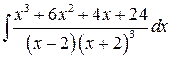 
Решение:
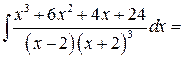
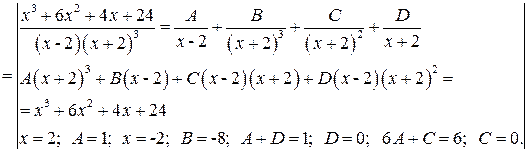
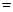
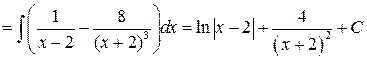
Задача №6:
Вычислить интеграл: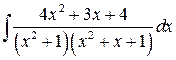 
Решение:
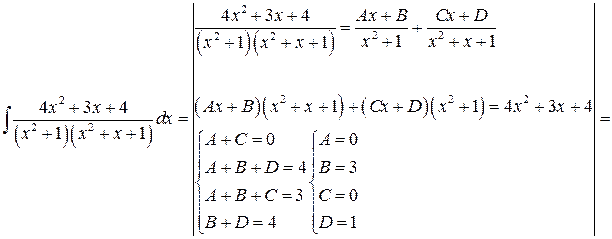
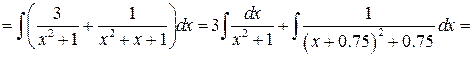
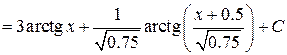
Задача №7:
Вычислить интеграл: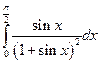 
Решение:
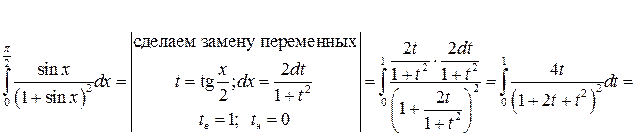
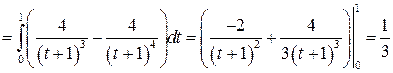
Задача №8:
Вычислить интеграл: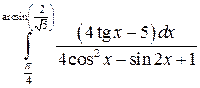 
Решение:
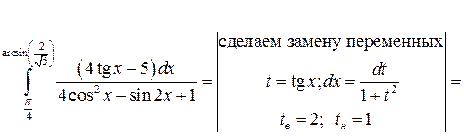
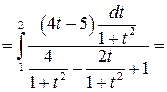
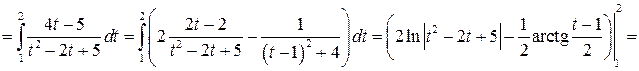
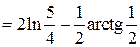
Задача №9:
Вычислить интеграл: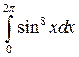 
Решение:
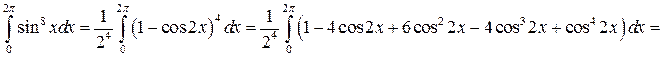
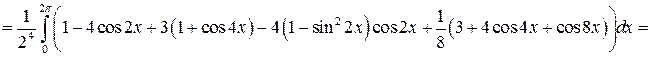
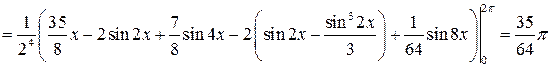
Задача №10:
Вычислить интеграл: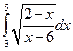 
Решение:
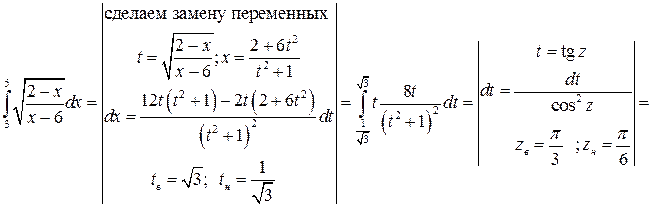
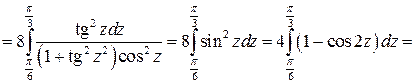
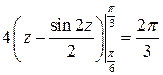
Задача №11:
Вычислить интеграл: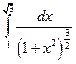 
Решение:
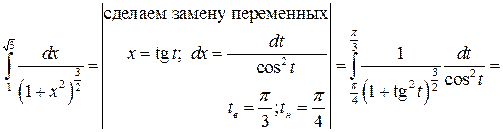
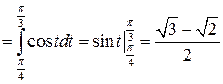
Задача №12:
Вычислить интеграл: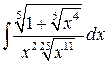 
Решение:
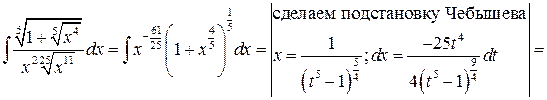
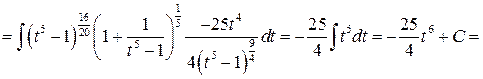
1. Функции многих переменных
