8.2.1. Формула Ньютона-Лейбница
Для вычисления определенного интеграла от непрерывной на отрезке [ a; b ] функции f (x) в том случае, когда может быть найдена ее первообразная F (x) служит формула Ньютона-Лейбница:
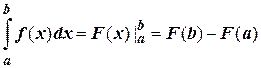 ,
,
т.е. определенный интеграл равен разности значений любой первообразной при верхнем и нижнем пределах интегрирования.
При интегрировании четных и нечетных функций в симметричных пределах интегрирования используют формулу
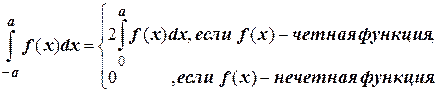
Пример. Вычислить определенные интегралы.
1) 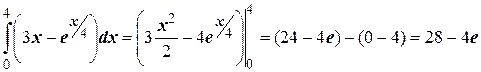 .
.
2) 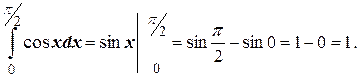
8.2.2. Метод подстановки
При вычислении определенного интеграла методом замены переменной (метод подстановки) данный интеграл преобразуется с помощью подстановки t=y (x) или x=j (t) в определенный интеграл относительно новой переменной интегрирования t. При этом старые пределы интегрирования a, b заменяются новыми переделами интегрирования a и b соответственно, которые находятся из исходной подстановки.
Из первой подстановки новые пределы интегрирования вычисляются непосредственно: a=y (a), b=y (b). Из второй подстановки новые пределы интегрирования находятся путем решения уравнений j (a) =a, j (b) =b относительно a и b.
Таким образом, имеем
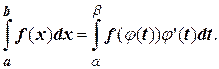
Здесь предполагается, что функции j (t) и j΄ (t) непрерывны на отрезке [ a; b ], а функция f (j (t)) определена и непрерывна на отрезке a£ t £ b.
Пример. Вычислим методом подстановки интеграл 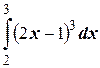 .
.
Решение. Введем новую переменную интегрирования с помощью подстановки t= 2 x– 1. Дифференцируя, получим dt= 2 dx, откуда dx=dt/ 2. Находим новые пределы интегрирования: подставляем в соотношение t= 2 x– 1значения x = 2, х = 3. Тогда получим α= 3, β= 5. Следовательно,
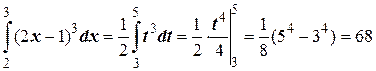 .
.
В дальнейшем при решении методом подстановки будем использовать форму записи как в неопределенном интеграле, используя вертикальные скобки.
8.2.3. Интегрирование по частям
Если функции u=u (x) и v=v (x) имеют непрерывные производные на отрезке [ a; b ], то для вычисления определенного интеграла используют формулу 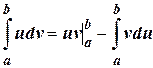 , которая называется формулой интегрирования по частям для определенного интеграла.
, которая называется формулой интегрирования по частям для определенного интеграла.
Пример. Вычислить интеграл 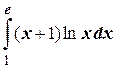 .
.
Решение. Положим 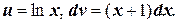 Тогда
Тогда 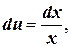
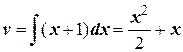 По формуле интегрирования по частям имеем
По формуле интегрирования по частям имеем
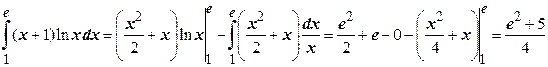 .
.
 2015-03-07
2015-03-07 662
662








