1. Пусть 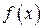 — функция, интегрируемая на
— функция, интегрируемая на  , и удовлетворяющая на этом отрезке соотношению
, и удовлетворяющая на этом отрезке соотношению 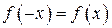 (такую функцию называют четной); тогда
(такую функцию называют четной); тогда
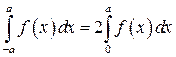
2. Пусть 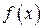 — функция, интегрируемая на
— функция, интегрируемая на  , и удовлетворяющая на этом отрезке соотношению
, и удовлетворяющая на этом отрезке соотношению 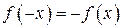 (такую функцию называют нечетной); тогда
(такую функцию называют нечетной); тогда
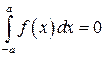
Замена переменного в определенном интеграле
Формула
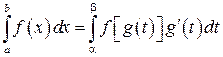
действительна при следующих условиях:
1. Функция 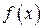 непрерывна на отрезке
непрерывна на отрезке 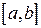 ;
;
2. Отрезок 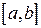 является множеством значений функции
является множеством значений функции 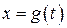 , определенной на отрезке
, определенной на отрезке 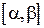 ;
;
3. 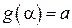 ;
; 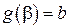 .
.
 2015-04-30
2015-04-30 290
290








