Пусть функция 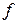 определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Функция
. Функция 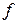 называется дифференцируемой по
называется дифференцируемой по  , если существует предел разностного отношения
, если существует предел разностного отношения
 (5.1)
(5.1)
этот предел называется частной производной функции 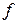 (по
(по  ) в точке
) в точке  и обозначается
и обозначается 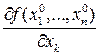 или
или 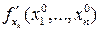 .
.
Таким образом, частная производная функции 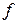 равна обыкновенной производной функции действительного переменного
равна обыкновенной производной функции действительного переменного  , которая получается из
, которая получается из 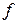 , если переменные
, если переменные 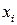 для
для 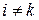 положить равными
положить равными  .
.
Для нахождения производной более высоких порядков, например порядка 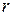 , применяется специальная формула (5.2). Эта формула получается в результате индукции при рассмотрении частных производных более низкого порядка.
, применяется специальная формула (5.2). Эта формула получается в результате индукции при рассмотрении частных производных более низкого порядка.
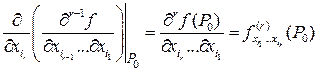 (5.2).
(5.2).
Рассмотрим геометрический смысл частной производной на примере функции 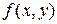 , которая дифференцируема по каждой из переменных в точке
, которая дифференцируема по каждой из переменных в точке 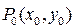 . По определению
. По определению  есть число, равное
есть число, равное 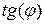 , где
, где 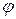 - угол между касательной к кривой пересечения плоскости П и графика функции
- угол между касательной к кривой пересечения плоскости П и графика функции 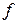 и плоскостью
и плоскостью  (см. рисунок ____). Аналогично и с
(см. рисунок ____). Аналогично и с 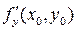 .
.
 2015-04-30
2015-04-30 274
274








