2015-04-20
800
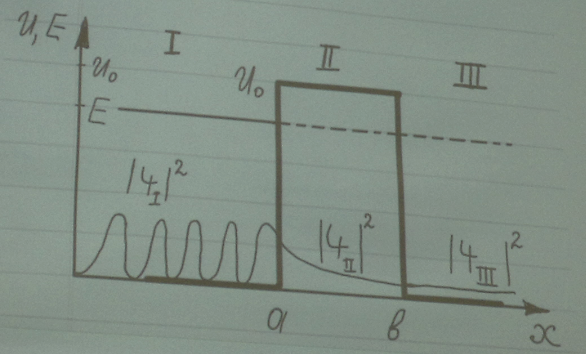
Пусть частица движется слева на право, встречая на своем пути потенциальный барьер высотой U0 и шириной (b – a). Зададим потенциальную функцию:(рис 1)
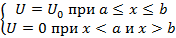
По классике – частица, налетающий на барьер справа из области I не может попасть в область III, для неё барьер непроницаем.
По квантовым представлениям – происходит частичное «просачивание» частица в область II. При достаточно тонком потенциальном барьере частица имеет шанс попасть в область III, недоступное для «классических» частиц. Такое просачивание через потенциальный барьер носит название туннельного эффекта и играет существенную роль в ряде физических явлений. Математическое туннельного эффекта приводит к необходимости решать уравнения Шредингера для областей I, II, III.
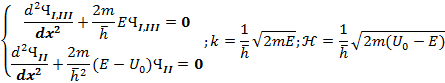
Граничные условия: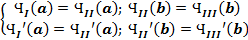 
Решения уравнений (2) имеют вид: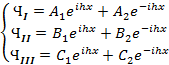 
Коэффициент прозрачности барьера, ширина (b – a) = I: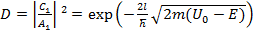 
D – вероятность прохождения, коэффициент прозрачности. R – вероятность отражения.
Оценим коэффициент прозрачности при: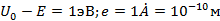 
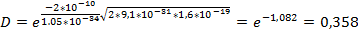
ОБЩАЯ ФОРМУЛА:
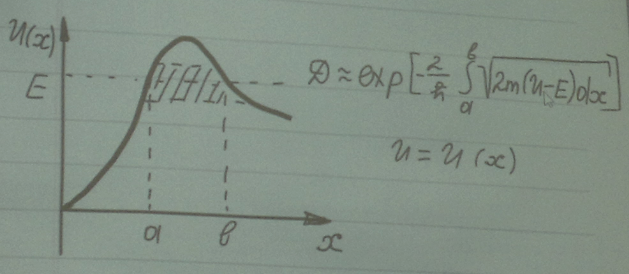
При преодолении потенциального барьера частицы как бы проходит через «туннель»:
