
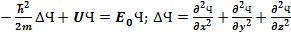
В одномерном случае: 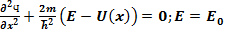 , где U(x) – потенциальная функция.
, где U(x) – потенциальная функция.
Рассмотрим самый простой случай - потенциальная функция соответствует потенциальной яме с бесконечно высокими стенками. Потенциальная функция:(рис 1)
Естественными граничными условиями для такой ямы будут равенства: 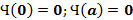
Для промежутка 0<X<a уравнения (2) запишется в виде: 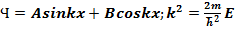
Первое из граничных условий сразу дает B = 0, второе приводит к соотношению:
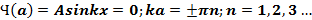
(n = 0 – отпадает, поскольку при этом получается, что пси-функция тождественно нулю, т.е. частицы нигде не находится.) 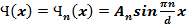
 Исключив k (6) и (8), найдем собственные значение энергии частицы:
Исключив k (6) и (8), найдем собственные значение энергии частицы: 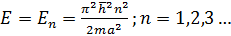
Итак, энергия частица в потенциальной яме может принимать только дискетные значения! Если частица локализована в пространстве в ограниченной области, то спектр значений энергии частицы дискретен, при отсутствии локализации – спектр энергий непрерывен.
(рис 2) Оценим расстояние между соседними уровнями для различных значений массы частицы “m” и ширины ямы “a”. Разность энергий двух соседних уровней равна:
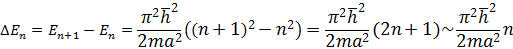
Молекула газа в сосуде: 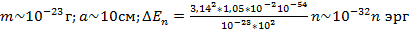
Столь густо расположенные энергетические уровни будут восприниматься как сплошной спектр энергии, хотя квантования будет иметь место, но на характере движения молекул сказываться не будет.
Свободный электрон в металле: 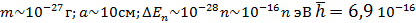 Эв*с
Эв*с
Это также очень маленькая дискретность, которая не скажется на энергетическом спектре и на характере движения электрона.
3) Электрон, локализованный в области атомных размеров:
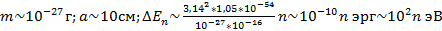
Амплитуда волновой функции в (9) – “An” из условия нормировки 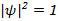 :
:
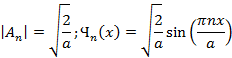
 2015-04-20
2015-04-20 946
946








