Для выборки, извлеченной из генеральной совокупности и представленной интервальным рядом (в первой строке указаны интервалы значений 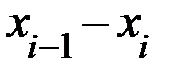 исследуемого количественного признака
исследуемого количественного признака 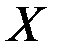 генеральной совокупности; во второй – частоты
генеральной совокупности; во второй – частоты 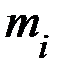 , т.е. количество элементов выборки, значения
, т.е. количество элементов выборки, значения 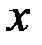 признака которых принадлежат указанному интервалу). Требуется:
признака которых принадлежат указанному интервалу). Требуется:
1) Построить полигон относительных накопленных частот
(кумулятивную кривую);
2) Построить гистограмму частот и гистограмму относительных частот;
3) Найти выборочную среднюю, выборочную дисперсию, моду и медиану;
4) Проверить на уровне значимости 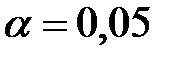 гипотезу о нормальном распределении признака
гипотезу о нормальном распределении признака 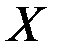 генеральной совокупности по критерию согласия Пирсона;
генеральной совокупности по критерию согласия Пирсона;
5) В случае согласованности с нормальным распределением найти с надежностью 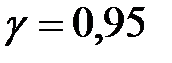 доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака
доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака 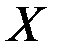 генеральной совокупности.
генеральной совокупности.
31.
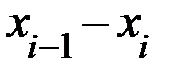
| 6,5-7,0 | 7,0-7,5 | 7,5-8,0 | 8,0-8,5 | 8,5-9,0 | 9,0-9,5 | 9,5-10 |
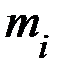
|
32.
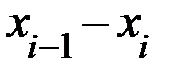
| 0,3-0,4 | 0,4-0,5 | 0,5-0,6 | 0,6-0,7 | 0,7-0,8 | 0,8-0,9 | 0,9-1 |
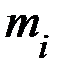
|
33.
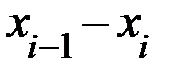
| 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 |
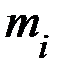
|
34.
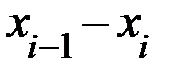
| 0,6-0,95 | 0,95-1,30 | 1,30-1,65 | 1,65-2,00 | 2,00-2,35 | 2,35-2,70 | 2,70-3,05 |
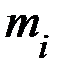
|
35.
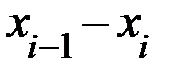
| 0,6-0,9 | 0,9-1,2 | 1,2-1,5 | 1,5-1,8 | 1,8-2,1 | 2,1-2,4 | 2,4-2,7 |
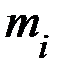
|
36.
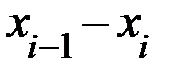
| 6,5-7,0 | 7,0-7,5 | 7,5-8,0 | 8,0-8,5 | 8,5-9,0 | 9,0-9,5 | 9,5-10 |
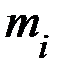
|
37.
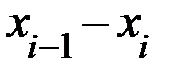
| 0,3-0,4 | 0,4-0,5 | 0,5-0,6 | 0,6-0,7 | 0,7-0,8 | 0,8-0,9 | 0,9-1 |
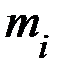
|
38.
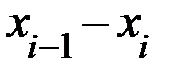
| 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 |
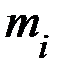
|
39.
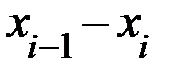
| 0,6-0,95 | 0,95-1,30 | 1,30-1,65 | 1,65-2,00 | 2,00-2,35 | 2,35-2,70 | 2,70-3,05 |
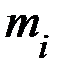
|
40.
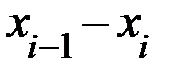
| 0,6-0,9 | 0,9-1,2 | 1,2-1,5 | 1,5-1,8 | 1,8-2,1 | 2,1-2,4 | 2,4-2,7 |
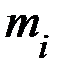
|
 2015-04-20
2015-04-20 381
381








