Примеры решения задач. Решение. Данный интеграл не является табличным

№1 Найти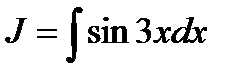

Решение. Данный интеграл не является табличным. Умножив на 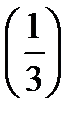и на (3) одновременно подинтегральное выражение, получим:

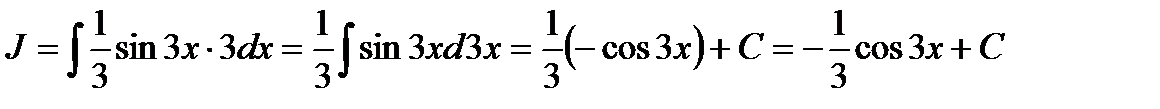
d3x

№ 2. Найти интеграл: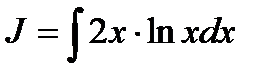

Решение. Используем интегрирование по частям, т.е используем формулу:

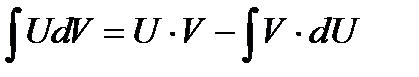
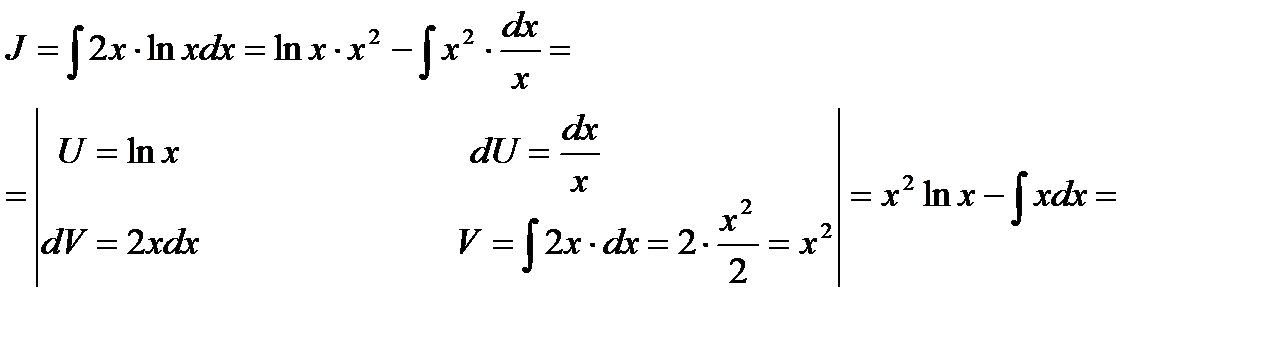
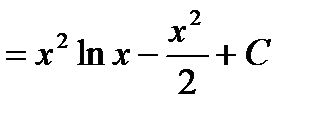
Имеем: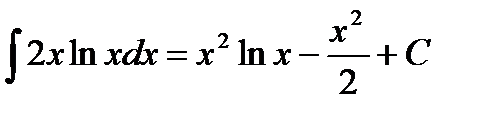

№ 3. Найти интеграл: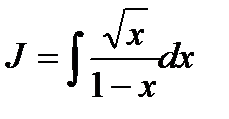

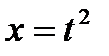
Решение: Используем подстановку, чтобы сделать подынтегральное выражение рациональным (без корня).

Итак,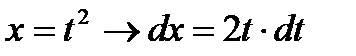

Тогда Jпримет вид:

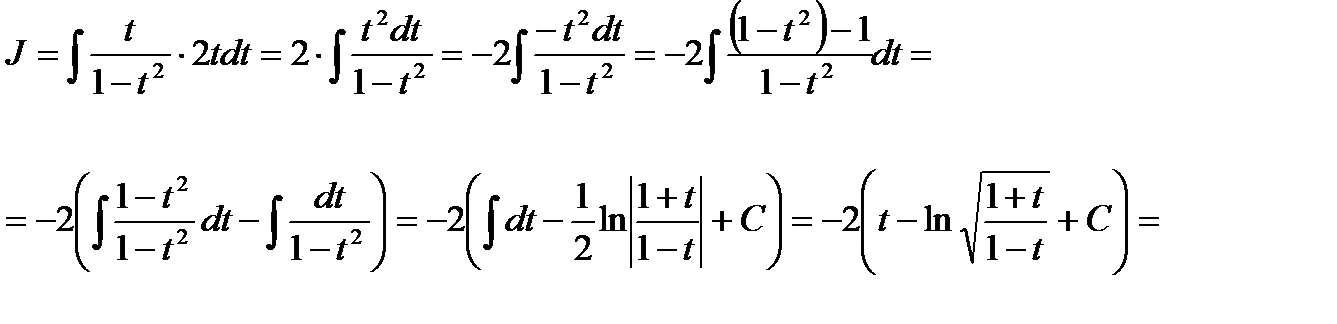
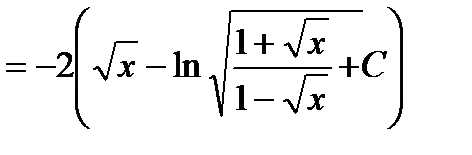
Использованы операции:

1. Замена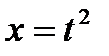

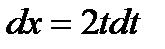
2.Вынесен постоянный множитель 2.

3.Умножим и разделим на (-1).

4.В числителе подынтегральной дроби прибавили (+1) и (-1).

5.Использовано свойство:

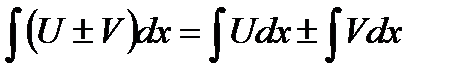
6.Применили табличные формулы:

.

7. Замена переменной по формуле (из подстановки)

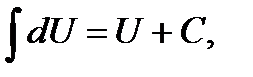
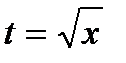
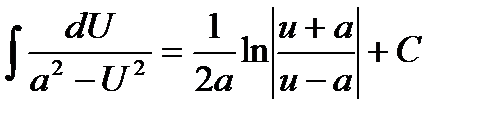
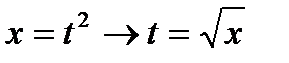7.3 Вопросы для самопроверки.

1. Дайте определение первообразной функции неопределённого интеграла. Приведите примеры.

2. Сформулировать свойства неопределённого интеграла.

3. В чём заключается геометрический смысл неопределённого интеграла?

4. Назовите основные методы интегрирования.

5. Решите: 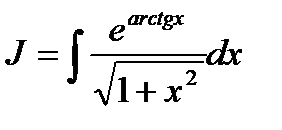методом подстановки.

6. Примените формулу интегрирования по частям к интегралу:

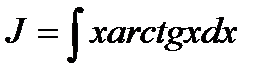
7. Объяснить, почему ∫x²cosx³dx решается способом подведения функции под знак дифференциала. Можно ли решить этот интеграл методом подстановки?