Примеры решения задач. Задача 1. Найти площадь фигуры, ограниченной параболой y=4x-x2 и осью ОХ

Задача 1. Найти площадь фигуры, ограниченной параболой y=4x-x² и осью ОХ.

Решение:

y

A

B

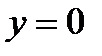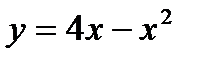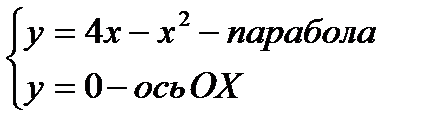
x

Решая систему, найдём точки пересечения: x=0; x=4.

Фигура OABO- криволинейная трапеция.

Значит, 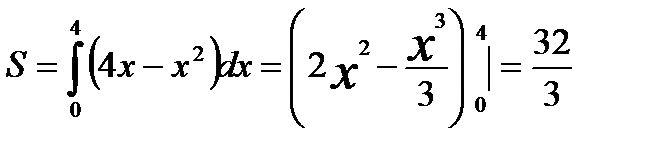(кв. ед)

Задача 2. Найти длину дуги кривой y²=x³ от x=0 до x=1, (y ³ 0).

Решение:

Дифференцируем уравнение кривой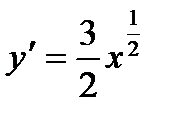

Имеем: 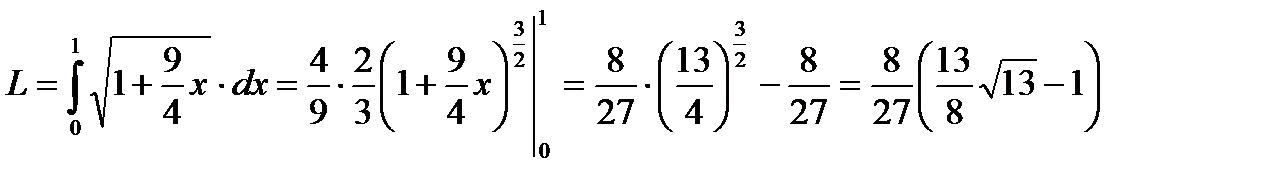(ед.)

Задача 3. Найти статический момент и момент инерции полуокружности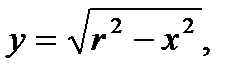

(-r £ x £ r) относительно оси OX.

Решение.

1.

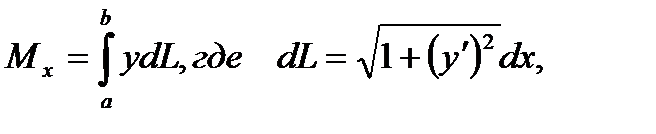
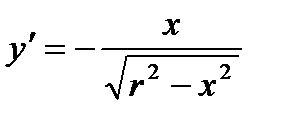
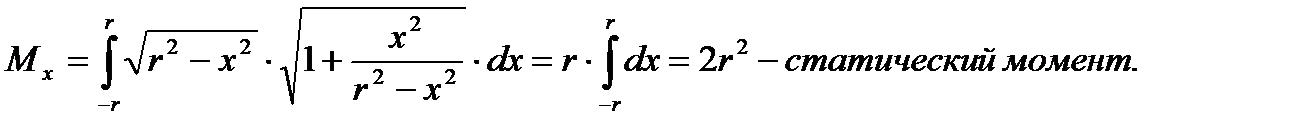
2.

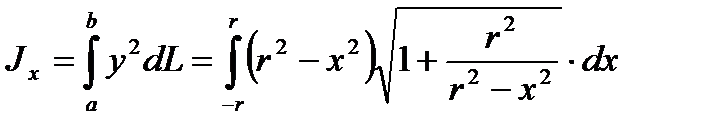
Введём подстановку

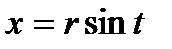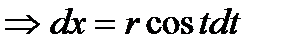. Если x=0, то t=0, если x=r, то .

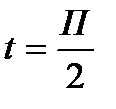Следовательно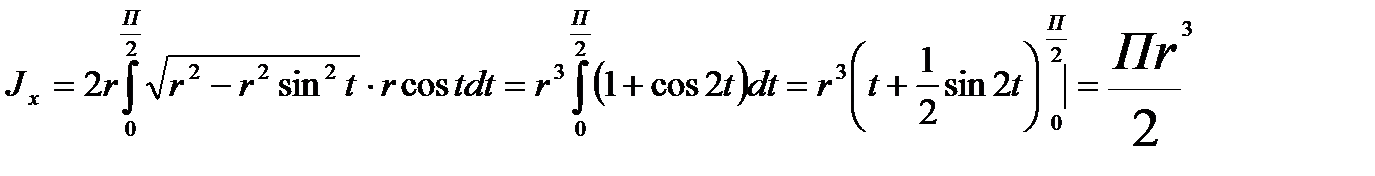

Задача 4. Найти площадь, заключённую внутри лемнискаты Бернулли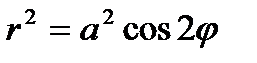

Решение: В силу симметрии достаточно вычислить одну четверть искомой площади, а затем учетверить результат.

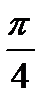y

x

По формуле 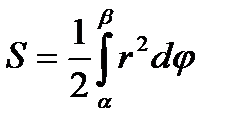имеем

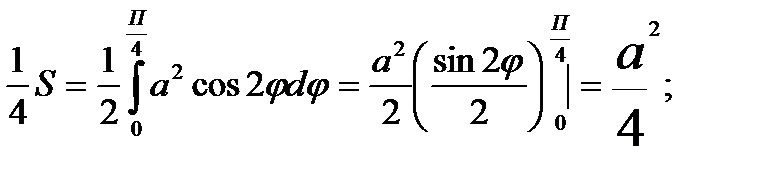
Отсюда S=a²

8.3 Вопросы для самопроверки.

1. Запишите формулу интегральной суммы функции f(x) на [a;b].
2. Сформулируйте определение определённого интеграла по [a;b]
3. Каков геометрический смысл

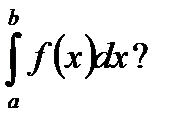
4. По какой формуле вычисляется 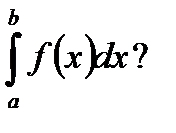Приведите примеры.

5. Дайте определение несобственного интеграла.

6. Является ли 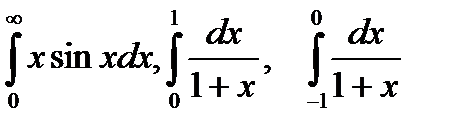несобственными?

7. Геометрический смысл несобственных интегралов.

8. В каких задачах используются определённые интегралы по отрезку [a;b] в геометрии?

В механике?