Тема 8. Определённыйинтеграл по отрезку

Определение: Определённым интегралом по отрезку [a;b]от функции f(x) называется предел интегральной суммы 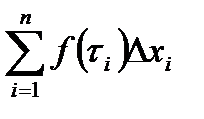, если этот предел существует и не зависит ни от деления отрезка [a;b]на части, ни от выбора точек t внутри каждой из частей при условии, что длина наибольшего из частичных отрезков (∆x_i) стремится к нулю, т.е

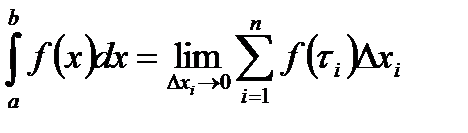
Числа a,bназываются соответственно нижним и верхним пределами интегрирования, т.е [a;b]-отрезок интегрирования.

Свойства определённого интеграла по [a;b].

1.

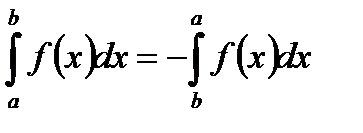
2.

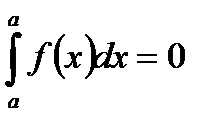
3.

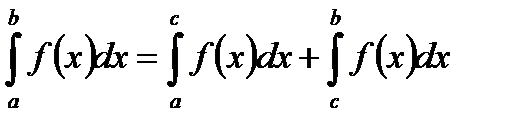
4.

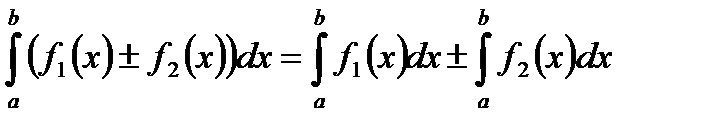
5. 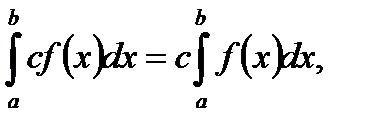С- постоянная

Правила вычисления определённого интеграла по [a;b]

функция для f(x),

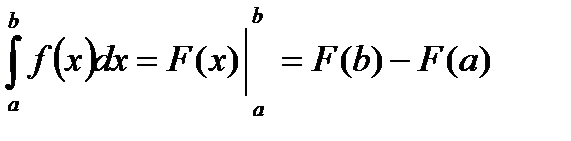1. - формула Ньютона-Лейбница, где F(x)- первообразная

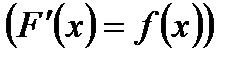2. 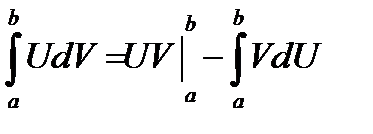- интегрирование по частям.

3. 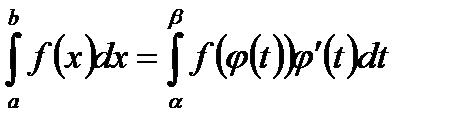, где x=j(t) функция непрерывная вместе со своей производной

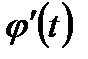на [a;b]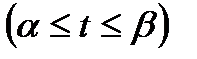

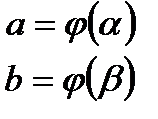
Например: Найти значение определённого интеграла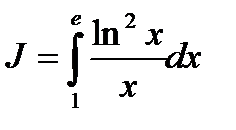

Решение:

Решаем методом подстановки

x		e
t

Положим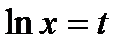

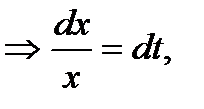
Тогда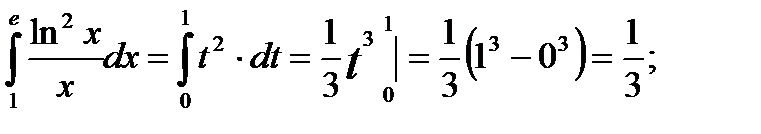

8.1 Несобственные интегралы.

К несобственным интегралам относятся:

1. Интегралы с бесконечными пределами интегрирования вида:

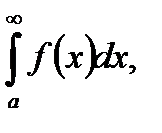
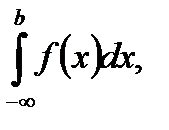
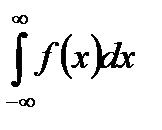
1. Интегралы от разрывных функций (от неограниченных функций).

Пример 1. 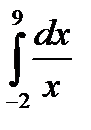- несобственный интеграл 2) типа, т.к на отрезке [-2;9]функция 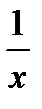терпит бесконечный разрыв в точке x=0.

Пример 2. Вычислить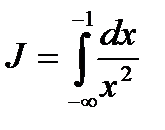

Решение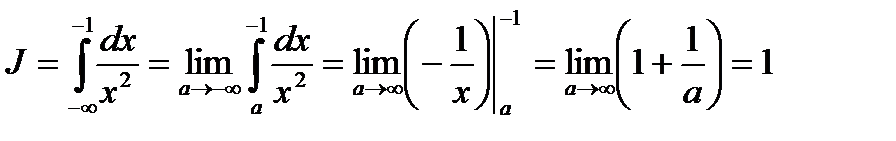

Пример 3. Вычислить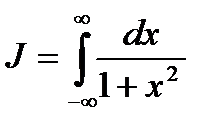

Решение: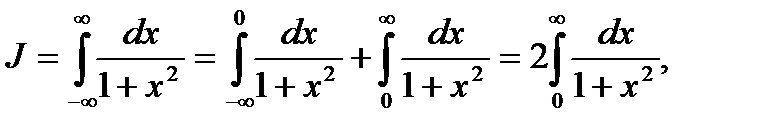

Т.к 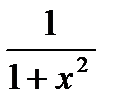- чётная функция.

Тогда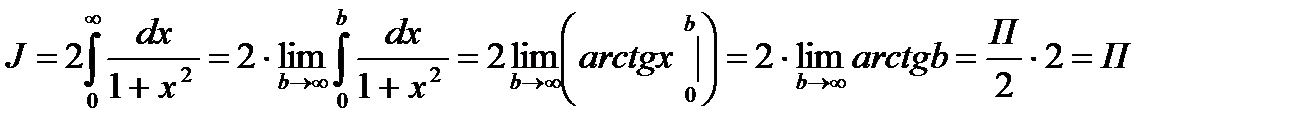

Замечание. Если предел несобственного интеграла существует и конечен, то несобственный интеграл называется сходящимся.

Если же предел не существует или равен бесконечности, то интеграл называется расходящимся.

8.2 Приложения определённого интеграла по [a;b]

1. 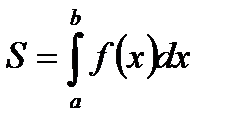-площадь криволинейной трапеции, где y=f(x)- кривая, ограничивающая криволинейную трапецию, aABb- криволинейная трапеция.

y

B

A

a

b

2. 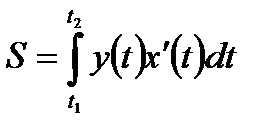- площадь криволинейной трапеции, если кривая задана

параметрически: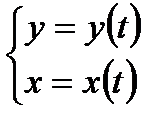

3. 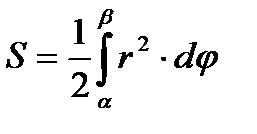- площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах, где r= r(a) - уравнение кривой.

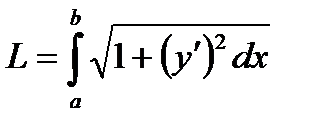1. вычисление длины дуги кривой y=f(x) на [a;b]

5. Вычисления объёма тела вращения.

y

a

b

x

Если криволинейная трапеция вращается вокруг оси OX, то объём тела вращения вычисляется по формуле:

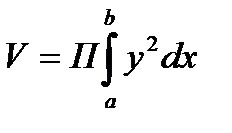
6. Статические моменты и моменты инерции дуги плоской кривой y=f(x), (a £ x £ b) вычисляются по формулам (соответственно):

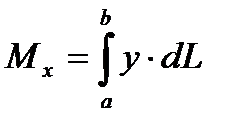
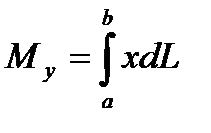
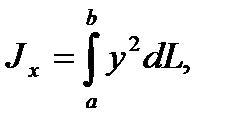
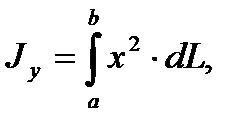
где 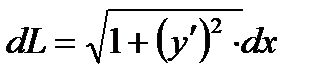- дифференциал дуги кривой y=f(x)

7. Координаты центра тяжести однородной дуги плоской кривой y=f(x) (a £ x £ b)

выражаются формулами:

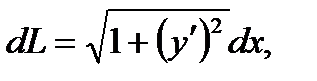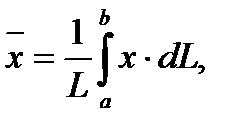где 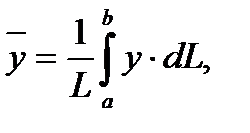L-длина дуги.