Основные формулы. 1. Определение криволинейного интеграла по длине дуги (1-го рода)

1. Определение криволинейного интеграла по длине дуги (1-го рода).

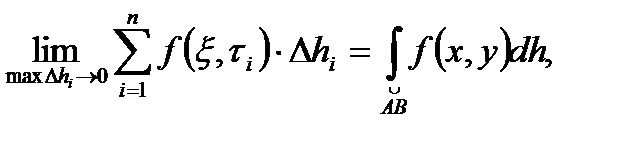
где h=AB, имеющая уравнение y= j(x)

dh-дифференциал дуги ABили h.

2.Вычисление криволинейного интеграла по длине дуги (1-го рода).

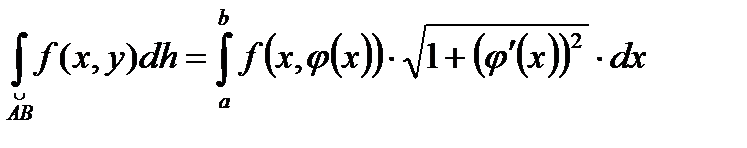
где 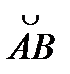имеющая уравнение y=j(x),

j^/(x)- производная y.

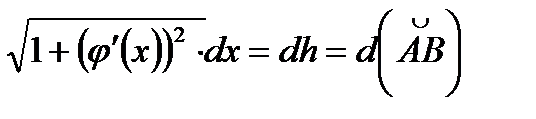
3.Определение криволинейного интеграла по координатам (2-го рода).

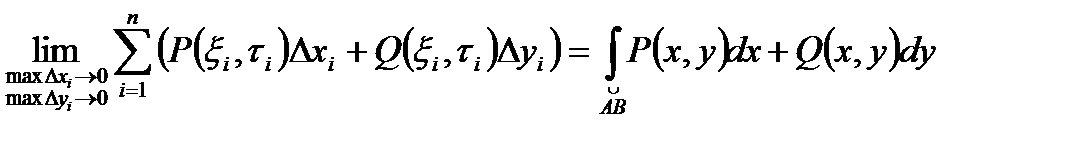
Криволинейный интеграл по координатам (II-го рода) есть работа, совершаемая переменной силой

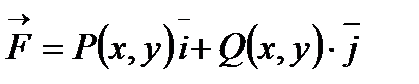на криволинейном пути AB(механическое толкование).

4.

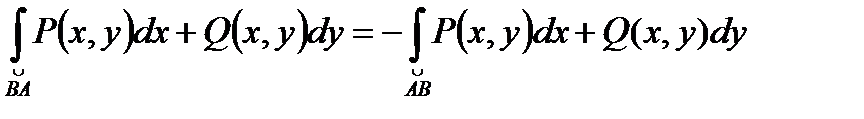
5.

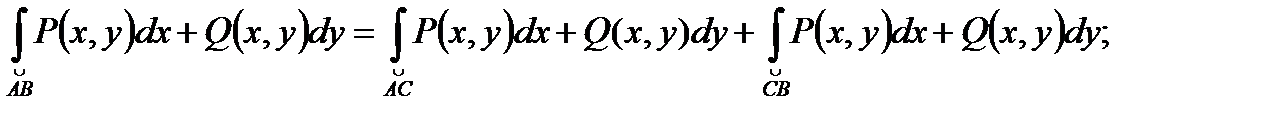
(A C B)

6.Криволинейный интеграл II-го рода (по координатам) вычисляется по формуле:

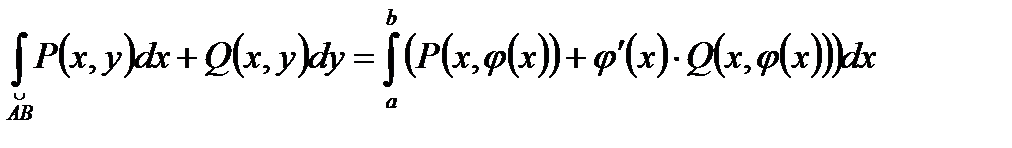
где 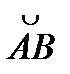представлена уравнением y=j(x), [a,b]-отрезок изменения x дуги AB.

7.

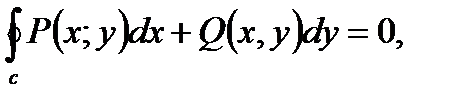
т.е криволинейный интеграл по любому замкнутому контуру равен нулю.

8. 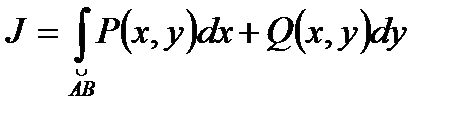не зависит от контура интегрирования между т. А и т. В, если выполняется тождественное равенство: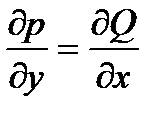

Этот факт используется в качестве наивыгоднейшего пути интегрирования (следует выбрать ломаную, соединяющую точки А и В, звенья которой параллельны осям (OX) и (OY).

Подынтегральное выражение 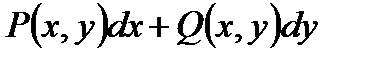при указанных условиях 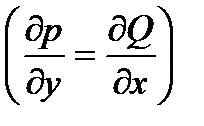является полным дифференциалом некоторой однозначной функции 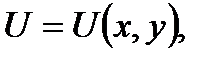т.е 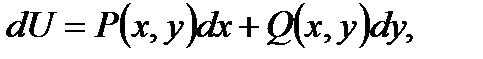а уравнение 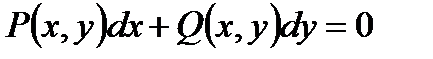называется дифференциальным уравнением в полных дифференциалах.

9. Площадь фигуры, ограниченной простым замкнутым контуром С, находится по формуле: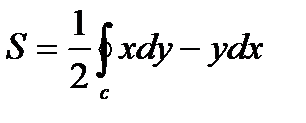

10.2. Примеры решения задач.

Задача 1. Вычислить криволинейный интеграл I-го рода по длине дуги

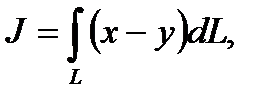где L- отрезок прямой от т. O(0;0) до B(4;3)

Решение:

Уравнение прямой имеет вид:

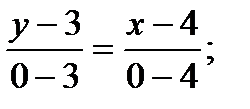или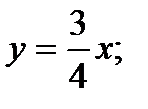

Находим 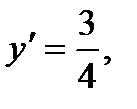тогда

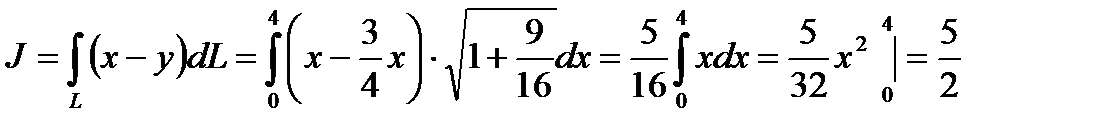
Задача 2. Вычислить площадь фигуры, ограниченной кривыми y= x², x= y²и 8xy=1.

Решение:

½

¼-

y

x

½

¼

B

A

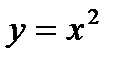
Решая совместно уравнения кривых находим координаты точек A и B:

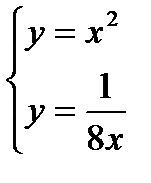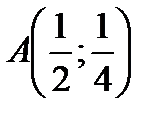
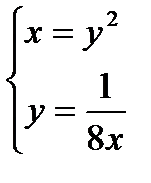Þ

Þ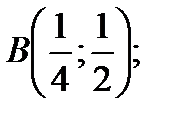

Значит, 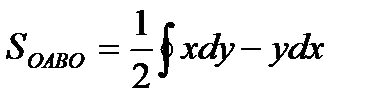или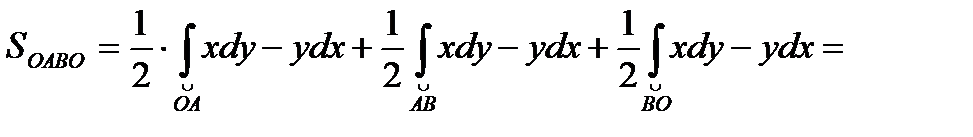

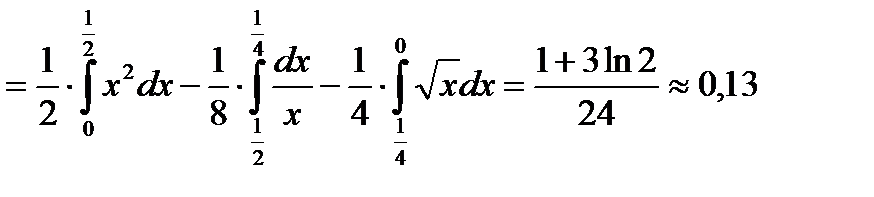
Это краткое решение. Более подробное решение имеет вид:

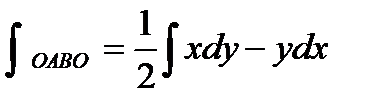или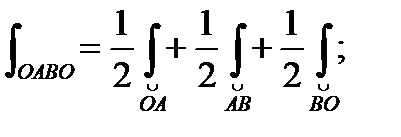

1. 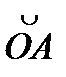-дуга параболы y= x²; dy=2xdx; тогда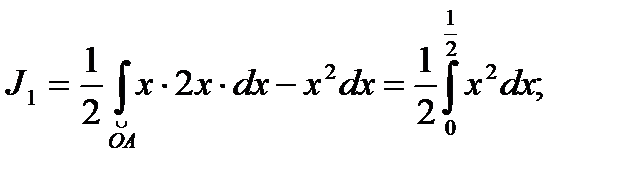

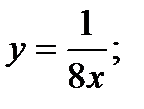2. - дуга кривой тогда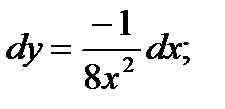

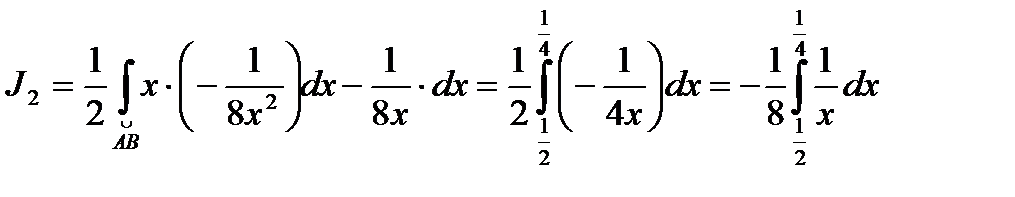
3. 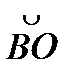-дуга кривой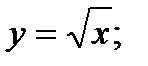 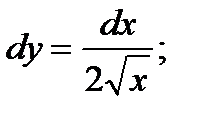тогда

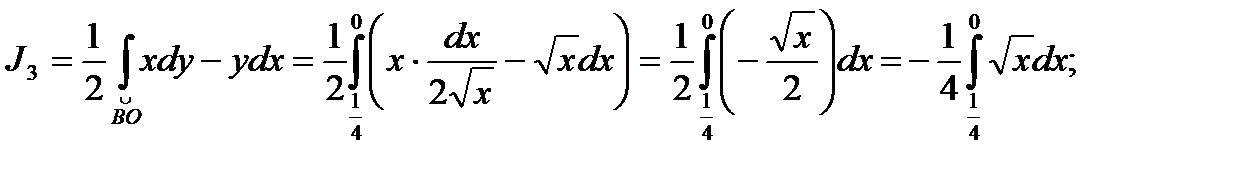
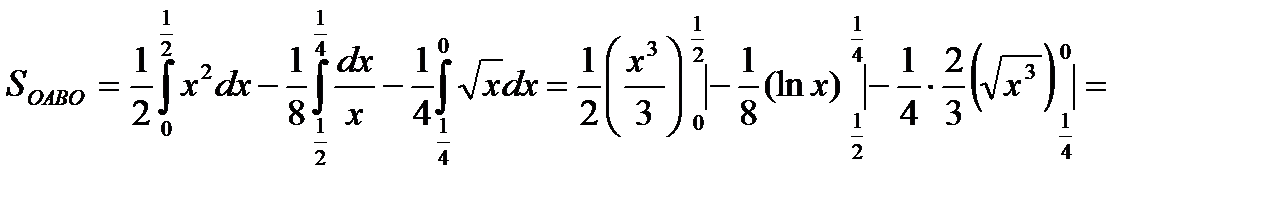
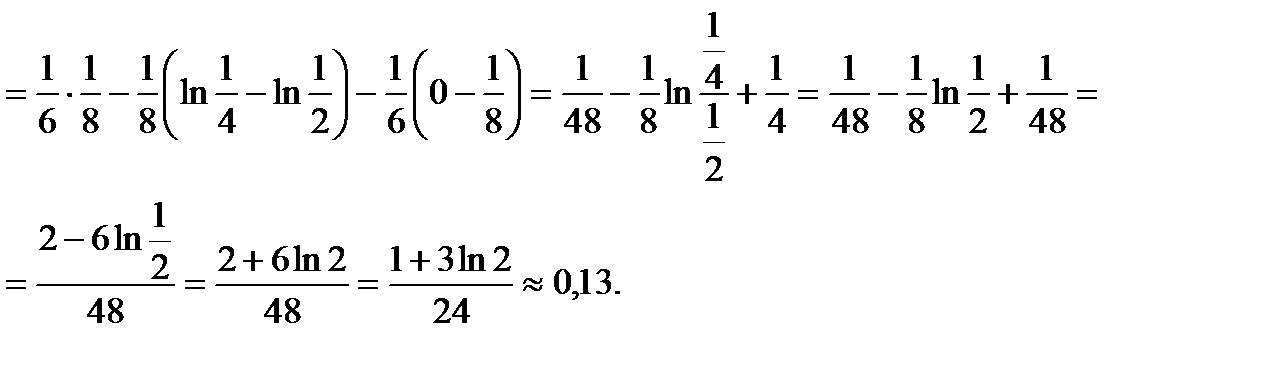
Задача 3. Дано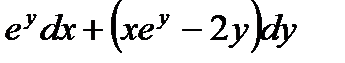

Проверить, что данное выражение является полным дифференциалом функции «U» и найти эту функцию.

Решение: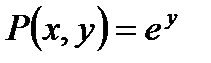

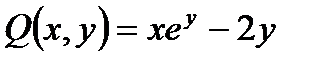
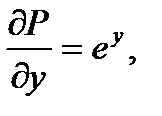
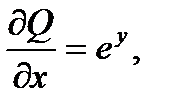
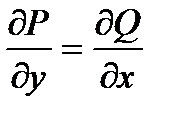- требование полного дифференциала выполняется и данное

выражение можно записать 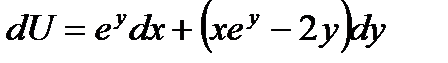, где U=U(x,y)- искомая функция.

Будем интегрировать dUпо ломаной OAM(см. рис.)

y. M (x;y)

O(0;0) A(x;0) x

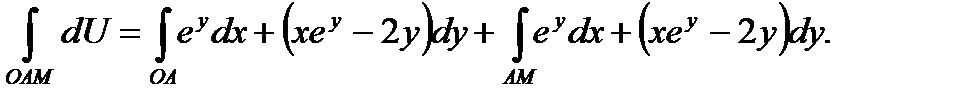
Учтя, что на пути [OA] y=0; dy=0 а на пути [AM] x=const, dx=0, получим:

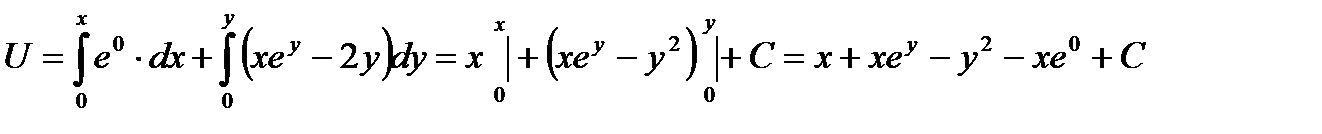
Ответ: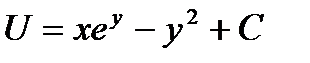

Задача 4. Найти центр тяжести дуги полуокружности 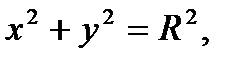лежащей в верхней полуплоскости. Плотность считать равной единице.

Решение: Из соображения симметрии ясно, что центр тяжести лежит на оси (OY), поэтому

X_c=0.

y

x

C

-R

R

B

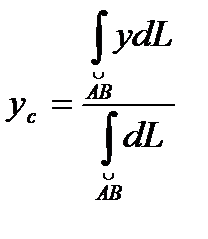Ордината , где dL-длина дуги.

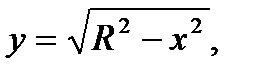
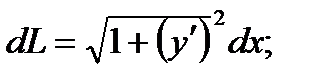
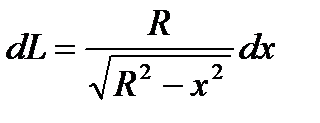
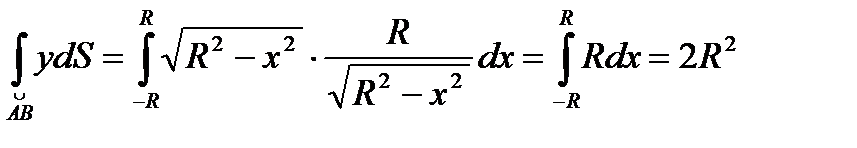
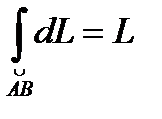- длина полуокружности, т.е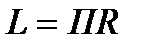

Тогда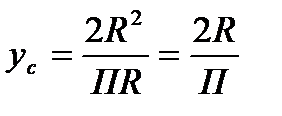

Ответ: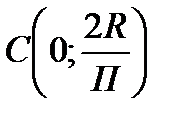

Вопросы для самопроверки.

1. Как определяется работа при движении точки в силовом поле?
2. Дайте определение криволинейного интеграла I-го и II-го рода по данной линии.
3. Запишите условие независимости криволинейного интеграла II-го рода (по координатам) от линии интегрирования.
4. Укажите наиболее удобный способ вычисления криволинейного интеграла II-го рода от полного дифференциала функции U.
5. Как вычисляется криволинейный интеграл I-го рода (по длине дуги)? Привести пример.
6. Как найти площадь плоской фигуры, ограниченной замкнутой линией?