Вариант 9
1. Бросается 5 монет. Какова вероятность того, что два раза выпадет герб?
2. Вероятность выиграть в рулетку равна 1/38. Игрок делает 190 ставок. С помощью какой таблицы можно найти вероятность того, что он выиграет не менее 5 раз?
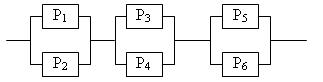
3. Определить надежность схемы, если Pi – надежность i – го элемента
4. Дан ряд распределения дискретной случайной величины. Определить значение второго центрального момента случайной величины.
| -4 | -2 | -14 | |||
| 0,1 | 0,2 | 0,1 | 0,3 | 0,2 | 0,1 |
5. Найти доверительный интервал для оценки математического ожидания m нормального закона с надежностью 0.9; зная выборочную среднюю 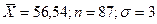 .
.
6. Задана матрица вероятностей перехода для цепи Маркова за один шаг. Найти матрицу перехода данной цепи за два шага 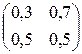 .
.
7. DX =2.5. Используя свойства дисперсии, найдите D(2X+5).
8. Рассматривается круглосуточная работа пункта проведения профилактического осмотра автомашин с четырьмя каналами (четырьмя группами проведения осмотра). На осмотр и выявление дефектов каждой машины затрачивается в среднем 0,8 часа. На осмотр поступает в среднем 40 машин в сутки. Машина, прибывшая в пункт осмотра, покидает пункт осмотра в случае, если в очереди на осмотр стоят более 7 машин. Определить вероятности состояний и характеристики обслуживания профилактического пункта осмотра. Найти число каналов при котором относительная пропускная способность пункта осмотра будет не менее 0,8.
 2015-04-30
2015-04-30 670
670








