2015-05-05
193
| RA | M | M | RB | ||||||||||
| A | B | ||||||||||||
| a | b | c | |||||||||||
| Q | |||||||||||||
| M | |||||||||||||
1. Определяем реакции опор.
SMA = M - M - RB×(a+b+c) = 0
RB =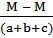 
= 0
SMB = RA×(a+b+c) + M - M = 0
RA =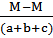 
= 
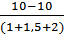= 0
Проверка: SY = RA+ RB = 0; 0 - 0 = 0
| I уч. | II уч. | III уч. | |||||||||||
| RA | RB | ||||||||||||
| MI | MII | MIII | |||||||||||
| xI | xII | xIII | |||||||||||
| QI | QII | QIII |
2. Построим характерный вид эпюр Q и M.
3. Выполним вычисления и уточним эпюры поперечной силы и изгибающего момента.
0≤xI≤a; SY=RA-QI=0 QI=RA= 0
RA×xI-MI=0 MI=RA×xI= 0
| Q | |||||||||||||
| M | |||||||||||||
a≤xII≤a+b; RA-QII=0 QII=RA= 0
RA×xII+M-M-MII=0; MII= RA×xII= 0
0≤xIII≤c; SY=QIII+RB=0 QIII=-RB= 0
MIII+RB×xIII=0 MIII=RB×xIII= 0
4. Построим эпюры по их аналитическим выражениям.
5. Произведем расчет на прочность балки по допускаемым натяжениям и подберем размеры поперечного сечения.
Mmax = 0
При [σ] = 160 МПа, Wx ≥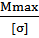 
, Wx ≥0
Wx ≥0 см3
Размеры поперечного сечения любые.
6. Определим перемещения и угол поворота заданного сечения.
yB =y0+θ0×(a+b+c)+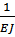 
×[ 
×RA×(a+b+c)3- 
×M×(b+c)2- ×M×c2]
θB =θ0+ 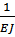×[ ×RA×(a+b+c)2-M×(b+c)-M×c]
