Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
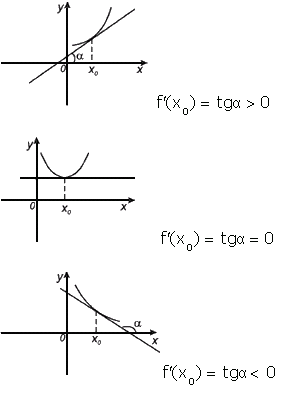
Рассмотрим график функции y = f (x):
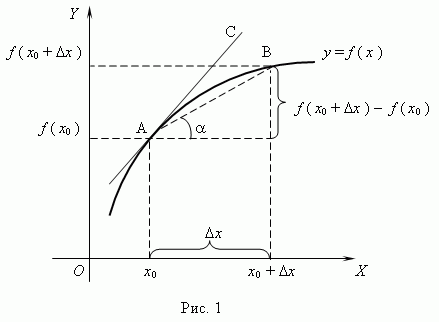
Из рис.1 видно, что для любых двух точек A и B графика функции: 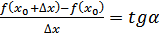 , где
, где 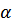 - угол наклона секущей AB. Таким образом, разностное отношение равно угловому коэффициенту секущей.
- угол наклона секущей AB. Таким образом, разностное отношение равно угловому коэффициенту секущей.
Если зафиксировать точку A и двигать по направлению к ней точку B, то 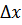 неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.
неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.
Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
В этом и состоит геометрический смысл производной.
11.Правила дифференцирования.
Пусть заданы две функции 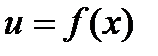 и
и 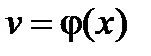 , которые имеют производные в точке
, которые имеют производные в точке 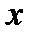 .
.
1. Производная алгебраической суммы равна алгебраической сумме производных. 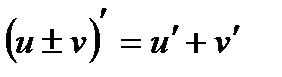 .
.
Покажем это. Пусть некоторая функция у, равная 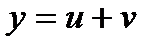 имеет приращение
имеет приращение 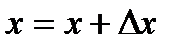 . Тогда функции
. Тогда функции 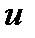 и
и 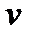 тоже должны получить приращения
тоже должны получить приращения 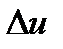 и
и 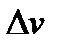 , соответственно. Новое значение
, соответственно. Новое значение 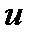 будет
будет 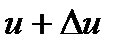 , а для
, а для 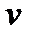 –
– 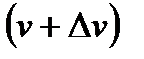 , следовательно,
, следовательно,
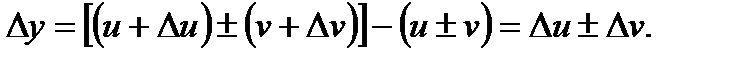
Найдем 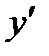 по определению (2) производной
по определению (2) производной
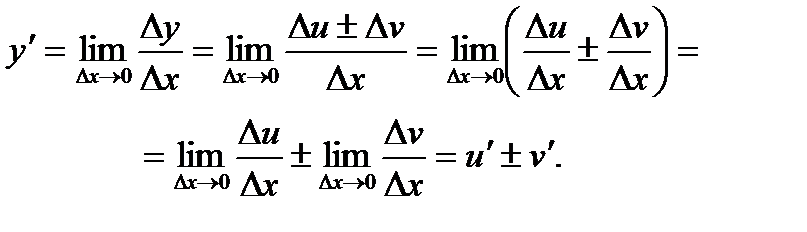 .
.
2. Производная произведения равна 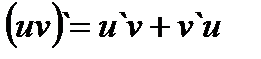 . Покажем справедливость этого равенства.
. Покажем справедливость этого равенства.
Если, как в первом случае, дать 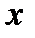 приращение
приращение 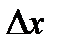 , то функции u и v также получат приращение, следовательно, и функция
, то функции u и v также получат приращение, следовательно, и функция 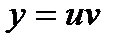 тоже изменится. Найдем
тоже изменится. Найдем 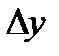 .
.
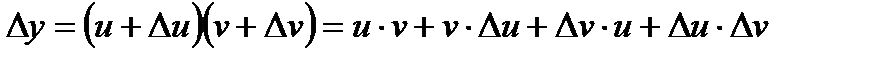 .
.
По определению производной
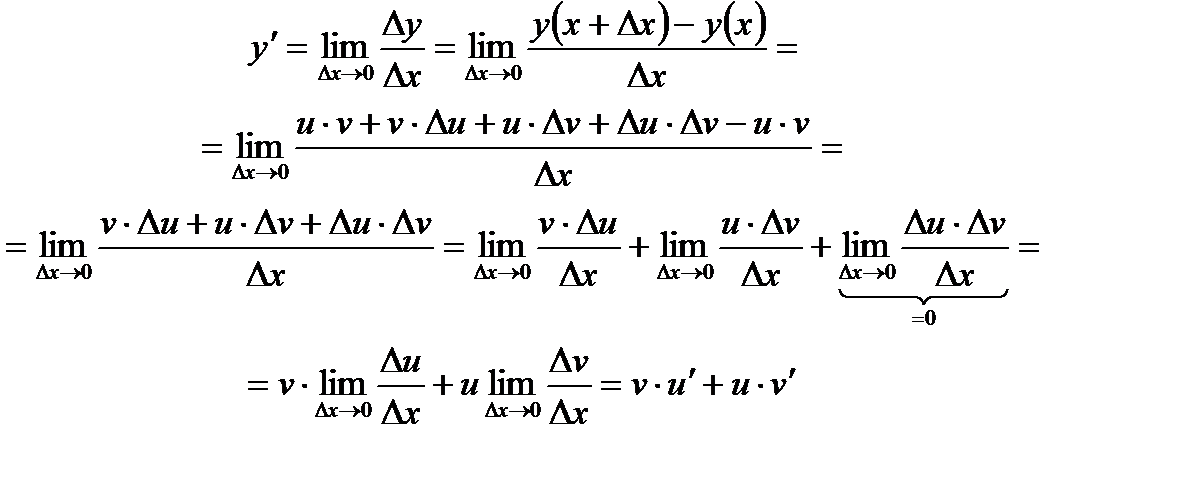
Если необходимо вычислить производную нескольких сомножителей, например, 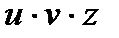 , если все три функции имеют производные в точке
, если все три функции имеют производные в точке 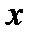 , используя правило вычисления производной для двух сомножителей, получим
, используя правило вычисления производной для двух сомножителей, получим
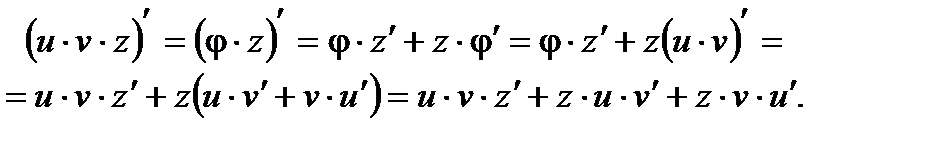
3. Производная частного. Рассмотрим функцию 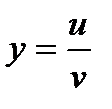 , причем, кроме существования производных в точке
, причем, кроме существования производных в точке 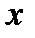 для функций
для функций 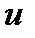 и
и 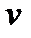 необходимо положить, что
необходимо положить, что 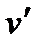 в точке
в точке 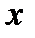 отлична от нуля.
отлична от нуля.
Найдем 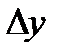 .
.
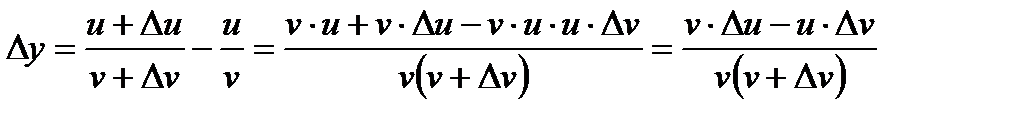
и тогда из определения производной имеем
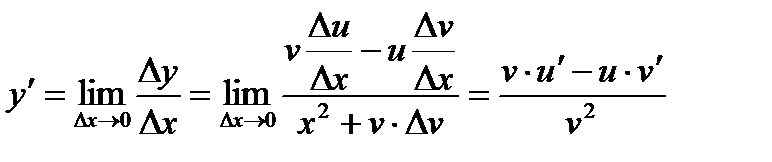 .
.
Пример. Показать, что 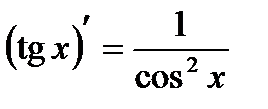 .
.
Решение. Используя производную частного
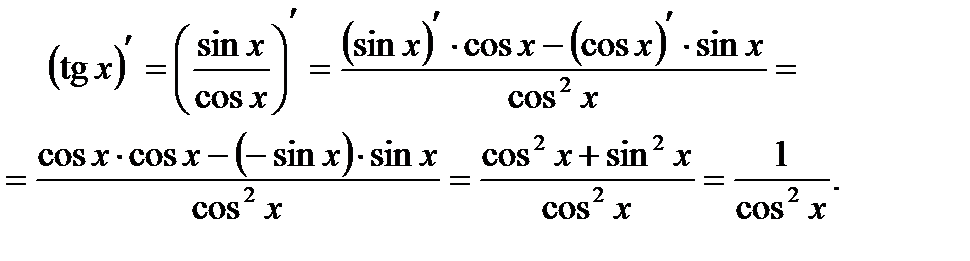
4. Производная сложной функции. Пусть дана 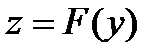 , где
, где 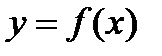 . Тогда имеет место теорема, которую приведем здесь без доказательства.
. Тогда имеет место теорема, которую приведем здесь без доказательства.
Теорема. Если функция 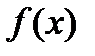 имеет в точке
имеет в точке 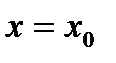 производную
производную 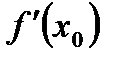 и функция
и функция 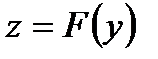 имеет в точке
имеет в точке 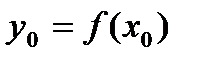 производную
производную 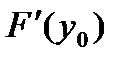 , тогда сложная функция
, тогда сложная функция 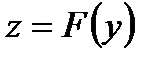 имеет в точке
имеет в точке 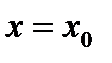 производную, равную
производную, равную
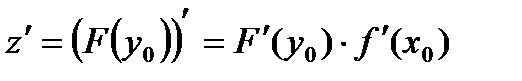 (3)
(3)
Пример. Найти производную функции 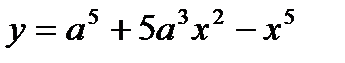 .
.
Решение. 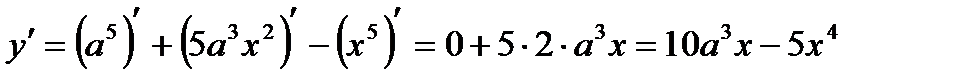 .
.
Пример. Найти производную функции 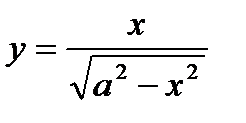 .
.
 2015-05-05
2015-05-05 691
691








