5. Логарифмическое дифференцирование. Пусть дана функция 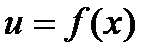 . При этом предполагается, что функция
. При этом предполагается, что функция 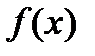 не обращается в нуль в точке
не обращается в нуль в точке 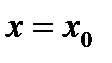 . Покажем один из способов нахождения производной функции
. Покажем один из способов нахождения производной функции 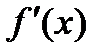 , если
, если 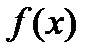 очень сложная функция и по обычным правилам дифференцирования найти производную затруднительно.
очень сложная функция и по обычным правилам дифференцирования найти производную затруднительно.
Так как по первоначальному предположению 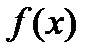 не равна нулю в точке, где ищется ее производная, то найдем новую функцию
не равна нулю в точке, где ищется ее производная, то найдем новую функцию 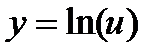 и вычислим ее производную
и вычислим ее производную
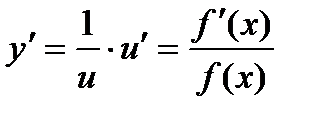 . (4)
. (4)
Отношение 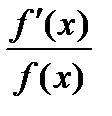 называется логарифмической производной функции
называется логарифмической производной функции 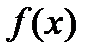 . Из формулы (4) получаем
. Из формулы (4) получаем
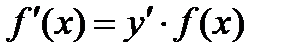 . (5)
. (5)
Формула (5) дает простой способ нахождения производной функции 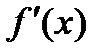 .
.
6. Производная обратной функции.
Теорема. Если 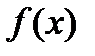 имеет в точке
имеет в точке 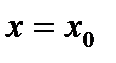 производную, отличную от нуля, тогда в этой точке обратная функция
производную, отличную от нуля, тогда в этой точке обратная функция 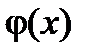 также имеет производную и имеет место соотношение
также имеет производную и имеет место соотношение
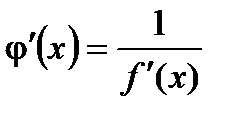 . (6)
. (6)
Пользуясь этой теоремой, найдем производные обратных тригонометрических функций.
1. 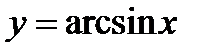 на интервале
на интервале 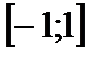 .
. 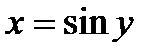 , тогда
, тогда 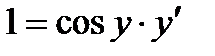 , откуда
, откуда 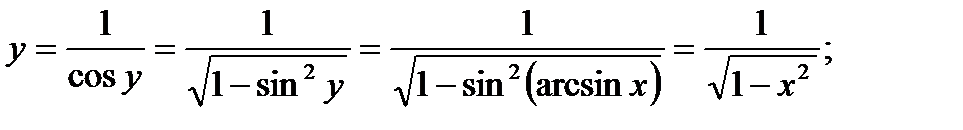 следовательно,
следовательно, 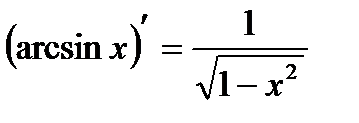 .
.
2. 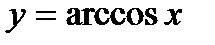 .
. 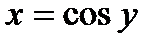 .
. 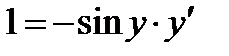 , откуда
, откуда
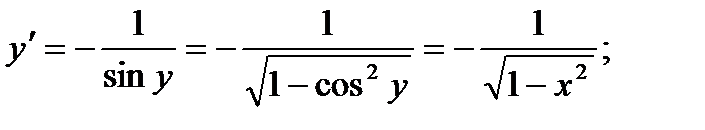
3. 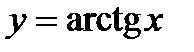 .
. 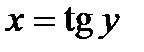 ;
; 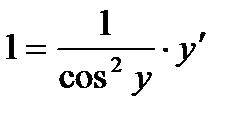 , откуда
, откуда
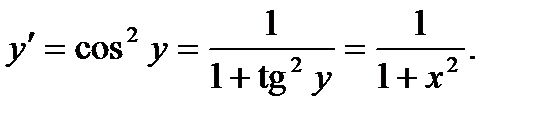
4. 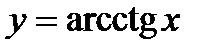 ;
; 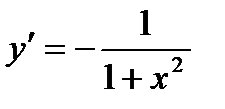 ;
;
5. 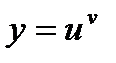 , где
, где 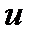 и
и 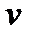 являются функциями от
являются функциями от 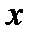 . Для нахождения
. Для нахождения 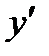 применим формулу (5). Для этого предварительно найдем функцию
применим формулу (5). Для этого предварительно найдем функцию
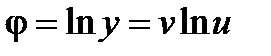
и ее производную
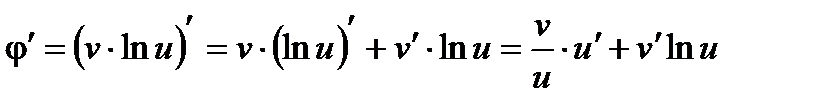 .
.
По формуле (5) получаем 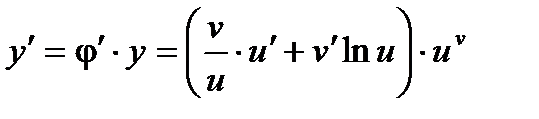 .
.
Эту же формулу можно получить иначе. Представим 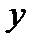 в виде
в виде
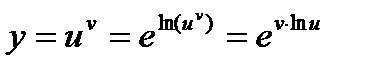
и найдем производную этой функции
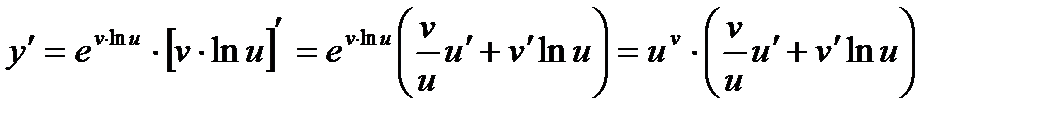 .
.
 2015-05-05
2015-05-05 551
551








