Теорема Ролля

Теорема Ро́лля утверждает, что если функция, имеющая производную на интервале, принимает в его концах равные значения, то её производная обращается в нуль в некоторой точке внутри интервала.

Формулировка Пусть дана непрерывная функция на отрезке 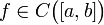, и для любого 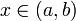существует конечная или бесконечная производная 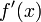. Тогда если 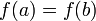, то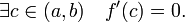

Следствия

-Многочлен 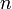-ой степени 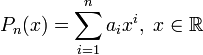может иметь не более 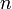различных корней.

- Если многочлен степени выше второй 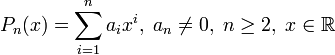имеет ровно 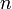различных корней, то его производная 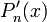имеет ровно 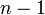корень.