Пусть функция  определена на отрезке
определена на отрезке 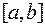 ,
,
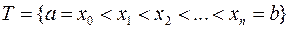 –
–
некоторое разбиение отрезка 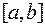 и
и 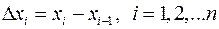 . Положим (см. рис.)
. Положим (см. рис.)
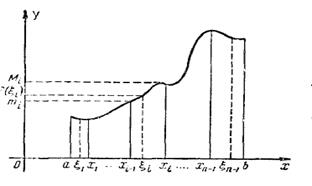
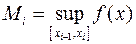 ,
, 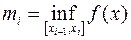 .
.
По определению числа 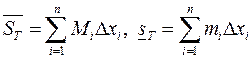 называются соответственно верхней и нижней интегральными суммами Дарбу.
называются соответственно верхней и нижней интегральными суммами Дарбу.
Свойство 1. Для любого разбиения 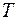 и для любой ограниченной функции
и для любой ограниченной функции  на отрезке
на отрезке 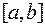 имеет место неравенство
имеет место неравенство
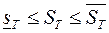 .
.
Мы будем называть разбиение 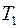 более мелким, чем разбиение
более мелким, чем разбиение 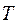 , если все точки разбиения
, если все точки разбиения 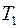 являются точками разбиения
являются точками разбиения 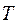 . То есть более мелкое разбиение
. То есть более мелкое разбиение 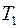 может быть получено из разбиения
может быть получено из разбиения 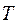 добавлением некоторых новых точек.
добавлением некоторых новых точек.
Свойство 2. Пусть 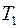 - разбиение более мелкое, чем разбиение
- разбиение более мелкое, чем разбиение 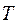 . Тогда
. Тогда
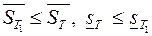 ,
,
то есть при измельчении разбиения верхняя сумма Дарбу может только уменьшится, а нижняя может только увеличится.
Так как разбиение 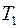 может быть получено из разбиения
может быть получено из разбиения 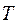 путем добавления к последнему новых точек, то, очевидно, что сформулированное свойство достаточно доказать в случае, когда к разбиению
путем добавления к последнему новых точек, то, очевидно, что сформулированное свойство достаточно доказать в случае, когда к разбиению 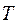 добавляется одна точка. Пусть эта точка
добавляется одна точка. Пусть эта точка 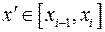 . Обозначим через
. Обозначим через 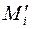 и
и 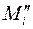 точные верхние грани функции
точные верхние грани функции  на сегментах
на сегментах 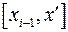 и
и 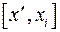 , через
, через 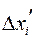 и
и 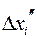 длины этих сегментов. Заметим, что
длины этих сегментов. Заметим, что 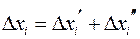 ,
, 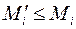 и
и 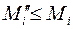 . Далее
. Далее
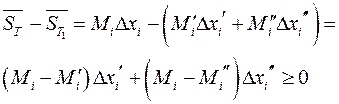 .
.
То есть 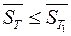 . Доказательство для нижних сумм проводится аналогично.
. Доказательство для нижних сумм проводится аналогично.
Свойство 3. Для любых разбиений 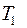 и
и 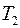 имеет место неравенство
имеет место неравенство
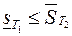 .
.
Добавим к точкам разбиения 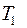 точки разбиения
точки разбиения 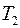 . Полученное разбиение обозначим через
. Полученное разбиение обозначим через 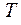 . Тогда из предыдущего свойства следует
. Тогда из предыдущего свойства следует
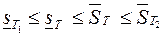 .
.
Свойство 4. Пусть 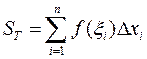 – интегральная сумма. Тогда имеет место неравенство
– интегральная сумма. Тогда имеет место неравенство
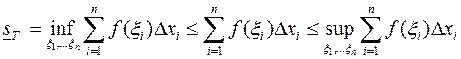
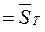 .
.
Это утверждение следует из того что
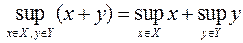 .
.
Свойство 5. Положим 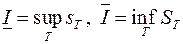 . Тогда
. Тогда 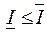 .
.
Это утверждение очевидно.
 2015-05-05
2015-05-05 7208
7208
