Необходимое и достаточное условие интегрируемости

Теорема. Для того чтобы ограниченная на некотором отрезке функция была интегрируема на этом отрезке, необходимо и достаточно, чтобы

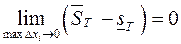. (1)

Условие (1) означает, что для любого 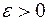найдется такое 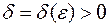, что 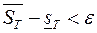для любого разбиения 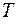такого, что .

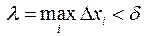Необходимость. Пусть ограниченная на отрезке 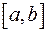функция интегрируема на этом отрезке и пусть

.

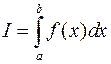Тогда для любого 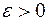найдется такое 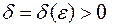, что если 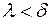, то

.

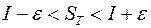Отсюда согласно свойству 4 интегральных сумм, получим

.

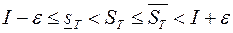Таким образом, если 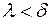, то 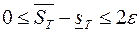, а это означает выполнение условия (1).

Достаточность. Пусть функция ограничена и имеет место (1). Из свойства 5 имеем 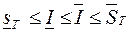, поэтому .

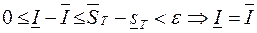Обозначая их общее значение через 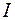, то есть 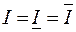, получим

.

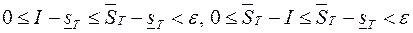Отсюда следует 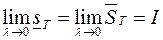и, в силу свойства 1 .

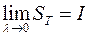Это и означает интегрируемость функции .

Функция, непрерывная на 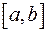, интегрируема на этом промежутке.

В дальнейшем понятие определенного интеграла 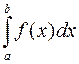будет расширено на неограниченные функции и на бесконечный промежуток.