Определение определенного интеграла

Зададим на конечном отрезке 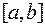функцию . Отрезок 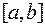разобьем на 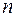частей точками

,

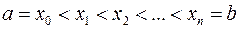и будем говорить, что произведено разбиение 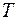отрезка 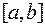. На каждом частичном отрезке 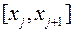выберем по произвольной точке 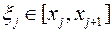и составим сумму

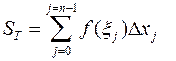
Ее называют интегральной суммой (Римана) функции па отрезке 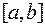, соответствующей разбиению 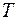. Интегральная сумма определена неоднозначно, потому что зависит от выбора .

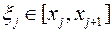Определение. Число 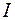называется пределом интегральных сумм 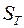, если для любого 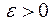можно указать такое 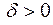, что для всех разбиений 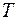, у которых 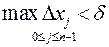, и независимо от выбора точек 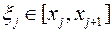имеет место неравенство

.

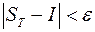Число 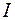называется определенным интегралом от функции на 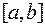и обозначается

.

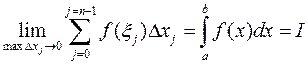Символ интеграла указывает на его происхождение: 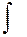является как бы вытянутой буквой 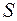— первой буквой слова summa; выражение, стоящее за знаком интеграла, показывает вид суммируемых слагаемых. Индекс при переменной в выражении под интегралом опущен, чем подчеркивается, что в процессе суммирования, завершающегося предельным переходом, переменная 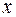принимает все значения в интервале 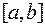. Числа, стоящие под и над символом интеграла, указывают концы интервала, на котором производилось суммирование. Функция называется подынтегральной функцией, выражение 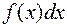– подынтегральным выражением, переменная 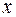– переменной интегрирования, число 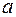– нижним, а число 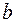– верхним пределами интегрирования.