Пусть на некотором отрезке [ a, b ] задана функция
y=f(x).
1. Разобьем отрезок [ a, b ] произвольным образом на n частей точками x1, x2,…, xn-1, при этом
a=x0<x1 <…<xi-1<xi<…< xn=b.
2. На каждом из полученных отрезков разбиения [ xi-1, xi ] (i=1, 2,…,n) выберем произвольным образом точку ξi, то есть 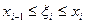 . Найдем значение функции в этой точке f(ξi).
. Найдем значение функции в этой точке f(ξi).
3. Составим сумму произведений вида 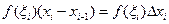 (функции f(x) в выбранных точках ξi на длину соответствующих отрезков разбиения):
(функции f(x) в выбранных точках ξi на длину соответствующих отрезков разбиения):
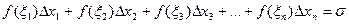 .
.
Эту сумму можно записать так:
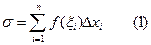 .
.
Сумма (1) называется интегральной суммой для функции y=f(x) на отрезке [ a, b ]. Эта сумма, вообще говоря, зависит от способа разбиения отрезка на части и от выбора промежуточных точек ξi. Очевидно каждому разбиению соответствует своя сумма.
Возьмем числовую последовательность положительных чисел δ1, δ2,…, δn,…, стремящуюся к нулю. Пусть разбиению, при котором длина наибольшего отрезка λ1<δ1, соответствует сумма σ1. Разбиению, при котором λ2<δ2, соответствует сумма σ2,…
Если для каждой последовательности разбиения, для которой δ1, δ2,…, δn,… стремится к 0, последовательность интегральных сумм σ1, σ2,…, σn,… стремится к некоторому числу I, одному и тому же при различном выборе точек ξi, то это число I называется пределом сумм σ, при λ, стремящемся к 0. На языке ξ, δ это определение звучит так:
 Опр. Число I называется пределом интегральных сумм
Опр. Число I называется пределом интегральных сумм 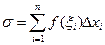 функции y=f(x) на отрезке [ a, b ], если для любого
функции y=f(x) на отрезке [ a, b ], если для любого 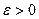 существует
существует 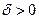 , что как только наименьшая из длин отрезков разбиения становится меньше δ, выполняется неравенство:
, что как только наименьшая из длин отрезков разбиения становится меньше δ, выполняется неравенство:
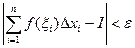 ,
,
как бы ни производилось разбиение отрезка и ни выбирались промежуточные точки ξi на отрезках разбиения.
 |
Опр. Если существует конечный предел I интегральных сумм σ, при стремлении наибольшего из отрезков разбиения λ к 0, то этот предел называется определенным интегралом функции f(x) на отрезке [ a, b ].
Обозначается 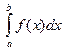 , а – нижняя граница интегрирования, b – верхняя граница интегрирования, х - переменная интегрирования, [ a, b ] – отрезок интегрирования.
, а – нижняя граница интегрирования, b – верхняя граница интегрирования, х - переменная интегрирования, [ a, b ] – отрезок интегрирования.
Итак, 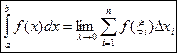
Поставим теперь задачу: выяснить условия, при которых интегральные суммы σ имеют конечный предел, то есть существует определенный интеграл.
Заметим, что для того чтобы функция f(x) была интегрируема на отрезке [ a, b ] (то есть существовал определенный интеграл от этой функции), необходимо чтобы она была ограничена на этом отрезке.
Действительно, если бы функция f(x) была на отрезке [ a, b ] неограничена, то при любом разбиении отрезка [ a, b ] на части, нашелся бы такой отрезок разбиения, на котором функция была бы неограничена. Тогда точку ξi на этом отрезке можно выбрать таким образом, что значение функции в этой точке f(ξi), а с ним и суммы σ будут стремиться к бесконечности. При этих условиях конечный предел I для интегральных сумм σ, очевидно, не существует.
Значит, необходимым условием интегрируемости функции является ее ограниченность на [ a, b ].
Но это условие не является достаточным, то есть не всякая ограниченная на отрезке [ a, b ] функция, интегрируема.
Например, функция Дирихле:
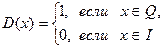 .
.
Эта функция ограничена на любом отрезке [ a, b ], так как множество ее значений 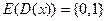 .
.
Но интегральные суммы σ=0, если будем выбирать точки ξi иррациональными, и σ =b-a, если будем выбирать ξi рациональными. Таким образом, интегральные суммы σ не имеют предела, то есть функция Дирихле не интегрируема.
В дальнейшем мы будем наперед предполагать рассматриваемую функцию f(x) ограниченной на отрезке [ a, b ], то есть 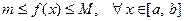 .
.
 2015-05-05
2015-05-05 806
806








