Теорема:
Для того чтобы функция f(x) была интегрируема на отрезке [ a, b ], необходимо и достаточно, чтобы
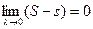 .
.
Доказательство:
1) Докажем необходимость.
По условию функция f(x) интегрируема на отрезке [ a, b ], значит и ограничена на нем. Составим нижнюю и верхнюю суммы Дарбу s и S. Обозначим интеграл 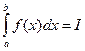 . Интегрируемость функции означает, что для любого
. Интегрируемость функции означает, что для любого 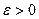 существует
существует 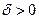 , такое, что как только наибольший из отрезков разбиения λ< δ, так будет выполняться неравенство
, такое, что как только наибольший из отрезков разбиения λ< δ, так будет выполняться неравенство 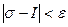 . Последнее неравенство равносильно неравенствам:
. Последнее неравенство равносильно неравенствам:
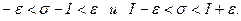
Как видим, 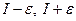 являются для интегральных сумм σ соответственно нижней и верхней границами. В то же время, согласно свойству сумм Дарбу, точной нижней границей для σ является s, а точной верхней – S. Поэтому
являются для интегральных сумм σ соответственно нижней и верхней границами. В то же время, согласно свойству сумм Дарбу, точной нижней границей для σ является s, а точной верхней – S. Поэтому
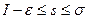 ,
, 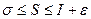 .
.
Учитывая это, получим: 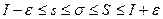 .
.
Следовательно, 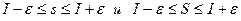 .
.
Таким образом 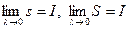 , тогда
, тогда 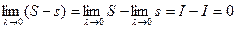 .
.
2) Докажем теперь достаточность.
Пусть 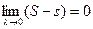 , докажем, что f(x) интегрируема на отрезке [ a, b ].
, докажем, что f(x) интегрируема на отрезке [ a, b ].
По условию, 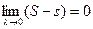 - это значит, для любого
- это значит, для любого 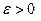 , существует
, существует 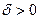 , что как только наибольший из отрезков разбиения
, что как только наибольший из отрезков разбиения 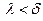 , выполняется неравенство
, выполняется неравенство 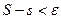 (1). Используя неравенства
(1). Используя неравенства 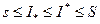 и учитывая последнее неравенство, получим
и учитывая последнее неравенство, получим
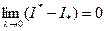 .
.
Следовательно, 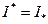 (они постоянны). Обозначим их общее значение через I=
(они постоянны). Обозначим их общее значение через I= 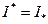 . Тогда
. Тогда 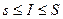 (2),
(2), 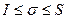 (3). Из неравенств (1), (2) и (3) следует, что
(3). Из неравенств (1), (2) и (3) следует, что 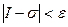 (4) (разность между
(4) (разность между 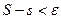 , то тем более разность чисел I и σ, заключенных между s и S, меньше
, то тем более разность чисел I и σ, заключенных между s и S, меньше  ),что означает, что
),что означает, что 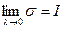 , а это значит, что функция f(x) является интегрируемой на [ a, b ].
, а это значит, что функция f(x) является интегрируемой на [ a, b ].
Замечание: Обычно эта теорема используется в другой форме.
Если обозначить колебание функции 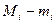 на отрезке [ xi-1, xi ] через wi, то
на отрезке [ xi-1, xi ] через wi, то 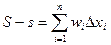 . Тогда условие существования интеграла будет таким:
. Тогда условие существования интеграла будет таким:
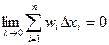 .
.
 2015-05-05
2015-05-05 498
498








