Наряду с интегральными суммами 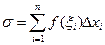 , составим другие суммы, более простые, но сходные с ними.
, составим другие суммы, более простые, но сходные с ними.
В силу ограниченности функции f(x) на каждом отрезке разбиения, найдутся числа
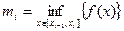 и
и 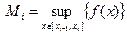 , i=1, 2,...,n.
, i=1, 2,...,n.
Составим суммы 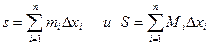 ,
,
где mi и Mi соответственно точные нижние и точные верхние границы множества значений функции f(x) на i- ом отрезке [ xi-1, xi ]. Эти суммы называются соответственно нижней и верхней интегральными суммами или нижней и верхней суммами Дарбу.
В частности, если функция f(x) непрерывна на отрезке [ a, b ], то s и S соответственно наименьшая и наибольшая из всех интегральных сумм, соответствующих данному разбиению отрезка [ a, b ] (точки ξi можно выбрать так, что f(ξi)= mi и f(ξi)= Mi по теореме Вейерштрасса).
Очевидно, 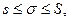 так как
так как 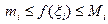 . При фиксированном разбиении отрезка [ a, b ] суммы Дарбу s и S будут постоянными числами, а σ будет переменной, так как точки ξi выбираются произвольно. За счет выбора точек ξi мы можем сделать интегральную сумму σ как угодно близкой к суммам Дарбу s или S. Значит при фиксированном разбиении суммы Дарбу s и S являются точными гранями интегральных сумм σ, то есть
. При фиксированном разбиении отрезка [ a, b ] суммы Дарбу s и S будут постоянными числами, а σ будет переменной, так как точки ξi выбираются произвольно. За счет выбора точек ξi мы можем сделать интегральную сумму σ как угодно близкой к суммам Дарбу s или S. Значит при фиксированном разбиении суммы Дарбу s и S являются точными гранями интегральных сумм σ, то есть
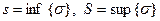 .
.
Суммы Дарбу обладают рядом свойств.
1°. Если к имеющимся точкам разбиения добавить новые точки, то нижняя сумма s может от этого только увеличиться, а верхняя сумма S – уменьшиться.
Доказательство:
Для доказательства этого свойства достаточно ограничиться присоединением к уже имеющимся точкам деления еще одной точки деления х / . Пусть она попадет внутрь отрезка [ xk-1 , xk ]. Пусть первому разбиению соответствует верхняя сумма S1, а второму разбиению, получившемуся из первого путем добавления новой точки х /, соответствует верхняя сумма S2. Нужно показать, что 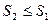 . Сумма S2 будет отличаться от S1 только тем, что вместо слагаемого Mk·∆xk будет иметь два слагаемых:
. Сумма S2 будет отличаться от S1 только тем, что вместо слагаемого Mk·∆xk будет иметь два слагаемых: 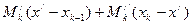 , где
, где 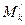 есть наибольшее значение функции на отрезке [ xk-1 , x/ ],
есть наибольшее значение функции на отрезке [ xk-1 , x/ ], 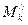 - наибольшее значение функции на отрезке [ x /, xk ]. Так как Mk есть наибольшее значение функции на всем отрезке [ xk-1, xk ], то, очевидно,
- наибольшее значение функции на отрезке [ x /, xk ]. Так как Mk есть наибольшее значение функции на всем отрезке [ xk-1, xk ], то, очевидно, 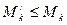 и
и 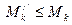 .
.
Тогда
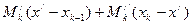
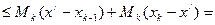
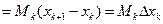 . Значит,
. Значит, 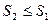 .
.
Аналогично можно доказать, что 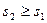 .
.
2°. Каждая нижняя сумма Дарбу не превосходит каждой верхней суммы, даже отвечающей другому разбиению отрезка.
Доказательство:
Разобьем отрезок [ a, b ] произвольным образом на n частей. Пусть этому разбиению соответствуют суммы Дарбу s1 и S1. Произведем другое разбиение, не связанное с первым. Ему пусть соответствуют суммы s2 и S2.
Нужно доказать, что 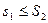 .
.
Возьмем третье разбиение отрезка, получившееся путем добавления к точкам разбиения второго, точек первого разбиения. Этому разбиению соответствуют суммы Дарбу s3 и S3, и по свойству 1° верхняя сумма 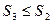 .
.
Рассуждая относительно нижних сумм Дарбу, получим, что 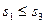 .
.
Итак, 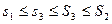 , следовательно
, следовательно 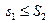 , что и требовалось доказать.
, что и требовалось доказать.
Учитывая это свойство, отметим, что множество всех нижних сумм Дарбу ограничено сверху, например любой верхней суммой. Значит это множество имеет точную верхнюю границу 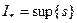 , и, кроме того,
, и, кроме того, 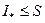 , какова бы ни была верхняя сумма S. Таким образом, множество верхних сумм Дарбу ограничено снизу числом
, какова бы ни была верхняя сумма S. Таким образом, множество верхних сумм Дарбу ограничено снизу числом 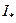 , следовательно имеет точную нижнюю границу
, следовательно имеет точную нижнюю границу 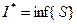 , причем
, причем 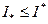 .
.
Сопоставляя все сказанное, имеем:
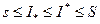 (1),
(1),
для любых сумм Дарбу.
 2015-05-05
2015-05-05 563
563








