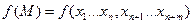
Теорема:
Пусть
1) 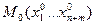 является точкой условного экстремума для функции
является точкой условного экстремума для функции 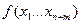 при условиях связи (*):
при условиях связи (*):
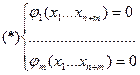
2) Функции 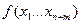 ,
,  имеют непрерывные частные производные первого порядка по всем переменным в некоторой окрестности точки
имеют непрерывные частные производные первого порядка по всем переменным в некоторой окрестности точки 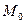 .
.
3) 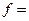
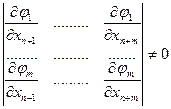 в точке
в точке 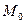 .
.
Тогда существуют числа 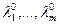 : точка
: точка 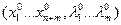 является стационарной точкой функции Лагранжа.
является стационарной точкой функции Лагранжа.
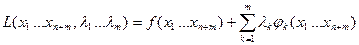 .
.
 2015-05-05
2015-05-05 273
273








