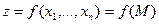
Определение: говорят, что в точке 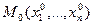 функция
функция 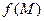 имеет максимум (минимум), если существует окрестность точки
имеет максимум (минимум), если существует окрестность точки 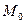 , для всех точек которой выполняется
, для всех точек которой выполняется 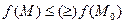 .
.
В случае строгого неравенства 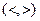 такой максимум (минимум) называется строгим. Точки максимума и минимума называются точками экстремума.
такой максимум (минимум) называется строгим. Точки максимума и минимума называются точками экстремума.
Теорема (о необходимом условии экстремума):
Пусть точка 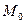 -точка экстремума для
-точка экстремума для 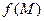 . Пусть функция
. Пусть функция 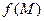 имеет конечные частные производные 1-го порядка по всем переменным в точке
имеет конечные частные производные 1-го порядка по всем переменным в точке 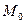 . Тогда все частные производные 1-го порядка равны нулю в точке
. Тогда все частные производные 1-го порядка равны нулю в точке 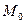 :
: 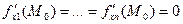 .
.
 2015-05-05
2015-05-05 349
349








