Пусть есть 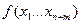
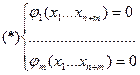 - условия связи.
- условия связи.
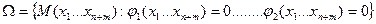 .
.
Определение: Говорят, что в точке 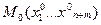 функция
функция 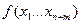 имеет условный минимум (максимум) при условиях связи (*), если существует окрестность
имеет условный минимум (максимум) при условиях связи (*), если существует окрестность 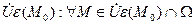 , такая, что выполнено условие
, такая, что выполнено условие 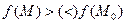 .
. 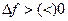 .
.
БИЛЕТ 18.
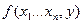 ,
, 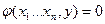
Теорема:
1) Пусть функции 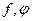 имеют в окрестности рассматриваемой точки
имеют в окрестности рассматриваемой точки 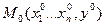 непрерывные производные 1-го порядка по всем переменным.
непрерывные производные 1-го порядка по всем переменным.
2) 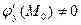
3) 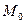 -точка условного экстремума.
-точка условного экстремума.
Тогда:
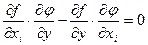 в точке
в точке 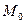
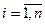 .
.
 2015-05-05
2015-05-05 363
363








